The definition of a logarithm is:
Subtraction of Logarithms Practice Problems & Solutions
Master logarithm subtraction with same and different bases. Practice problems include step-by-step solutions using quotient rule and base change formula.
- Apply the quotient rule: log_a(x) - log_a(y) = log_a(x/y) with identical bases
- Convert logarithms with different bases using change of base formula
- Solve complex logarithmic equations involving subtraction and simplification
- Identify when to use quotient rule versus base conversion methods
- Practice with real numbers like log_7(147) - log_7(3) step-by-step
- Build confidence solving advanced problems with variables and mixed bases
Understanding Subtraction of Logarithms
Subtraction of Logarithms
Where:
is the base of the exponent
is what appears inside the log, can also appear in parentheses
is the exponent we raise the log base to in order to obtain the number that appears inside of the log.
Subtraction of logarithms with identical base is based on the following rule:
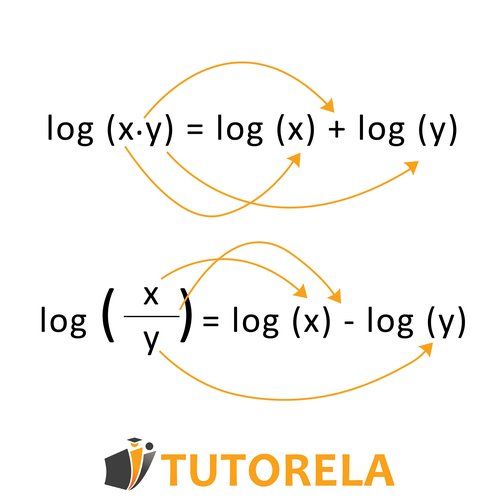
Subtraction of logarithms with different bases is performed by changing the base using the following rule:

Practice Subtraction of Logarithms
\( x=\text{?} \)
\( \log_{\frac{1}{2}}5-\log_{\frac{1}{2}}4\le\log_{\frac{1}{2}}x-\log_{\frac{1}{2}}3 \)
Examples with solutions for Subtraction of Logarithms
To solve the problem, we employ the property of logarithms for subtraction:
- Step 1: Recognize the expression .
- Step 2: Apply the logarithmic property for subtraction, .
- Step 3: Substitute into the property: .
By applying the property, we simplify the expression to . This is equivalent to . Therefore:
Therefore, the result of the expression is .
Answer:
To solve the problem of evaluating , we apply the properties of logarithms as follows:
- Step 1: Recognize that the expression uses a subtraction of logarithms with the same base: .
- Step 2: Use the logarithmic subtraction rule: .
- Step 3: Simplify using this rule: .
- Step 4: Perform the division: .
- Step 5: Therefore, .
Thus, the simplified and evaluated result is .
Answer:
To solve the problem, let's use the rules of logarithms:
- Step 1: Recognize that we are dealing with the subtraction of logarithms sharing the same base, which calls for the identity .
- Step 2: Apply this identity to the expression .
- Step 3: Realize that this can thus be expressed as a single logarithm: .
- Step 4: Simplify the fraction, yielding .
Therefore, the simplification results in the expression: .
This matches the correct answer from the given choices.
Answer:
To solve this problem, we'll begin by simplifying the given expression using logarithmic rules:
- Step 1: Simplify the first term :
Since , we can rewrite this as . Thus, . - Step 2: Simplify the second term :
Note . Therefore, . Thus, . - Step 3: Subtract the expressions:
Combine the terms using the difference rule:
. - Step 4: Simplify further:
Since , we can express this as .
Therefore, the simplified form of the expression is .
The correct choice is thus , matching with choice (1).
Answer:
To solve the problem , we need to apply the rules of logarithms:
- **Step 1: Simplify with the power rule**
Using the power rule . Since , we have . Thus, . - **Step 2: Apply the subtraction rule**
Now, the expression becomes . Using the subtraction rule: . - **Step 3: Simplify the fraction**
Calculate : it simplifies to 2 because .
Thus, the simplified expression is .
Using the provided answer choices, the correct answer matches choice , which corresponds to choice 2.
Therefore, the solution to the problem is .
Answer: