A circle has the equation: $$ x^2-6x+y^2-4y=7 $$ Use the completing the square method to find the center of the circle and its radius.

$$ (3,2),\hspace{6pt} R=\sqrt{20} $$

$$ (3,-2),\hspace{6pt} R=\sqrt{20} $$

A circle has the following equation: $ x^2-8ax+y^2+10ay=-5a^2 $ Point O is its center and is in the second quadrant ($$ a\neq0 $$) Use the completing the square method to find the center of the circle and its radius in terms of $$ a $$.

$$ O(4a,-5a),\hspace{4pt}R=-6a $$

$$ O(4a,5a),\hspace{4pt}R=6a $$

$$ O(4a,10a),\hspace{4pt}R=6a $$

$$ O(4a,-5a),\hspace{4pt}R=6a $$

Tangent to a circle - Examples, Exercises and Solutions

Understanding Tangent to a circle

Complete explanation with examples

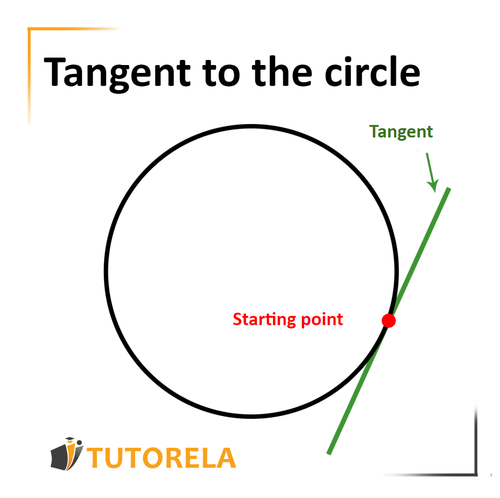
A tangent to a circle is a line that touches the circle at one point.

Tangent Theorem:

1) The tangent to the circle is perpendicular to the radius at the starting point

2) Every line perpendicular to the radius at its end is tangent to the circle

3) The angle between the tangent and any chord is equal to the circumferential angle that rests on that chord on the other side.

4) Two tangents to the circle that come out from the same point are equal to each other.

5) A segment that passes between the center of the circle and the point from which two tangents to the circle come out, cuts the angle between the tangents.

6) If from any point outside the circle, a tangent comes out and cuts the circle, then the product of the entire tangent on its outside is equal to the square of the tangent.

7) In the triangle that encloses the circle, the three bisectors of the angles of the triangle meet at a point in the center of the circle.

8) We can determine that a convex quadrilateral encloses a circle only if - the sum of two opposite sides in the square will be equal to the sum of the other two sides in the square.

Detailed explanation

Practice Tangent to a circle

Test your knowledge with 6 quizzes

Calculate the length of the arc marked in red given that the circumference is 12.

Examples with solutions for Tangent to a circle

Step-by-step solutions included

Exercise #1

A point whose distance from the center of the circle is _______ than the radius, is outside the circle.

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is greater than the center of the circle will necessarily be outside the circle.

Answer:

greater

Exercise #2

Where does a point need to be so that its distance from the center of the circle is the shortest?

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is less than the radius from the center of the circle will necessarily be inside the circle.

Answer:

Inside

Exercise #3

In which of the circles is the point marked inside of the circle and not on the circumference?

Step-by-Step Solution

Let's remember that the circular line draws the shape of the circle, and the inner part is called a disk.

Therefore, in diagram B, the point is located in the inner part, meaning inside the disk.

Answer:

Video Solution

Exercise #4

Identify which diagram shows the radius of a circle:

Step-by-Step Solution

Remember that a radius is a line segment connecting the center of a circle to any point on the circle itself.

In drawing C we can see that the line coming from the center of the circle indeed connects to a point on the circle itself, while in the other drawings the lines don't touch any point on the circle.

Therefore, C is the correct drawing.

Answer:

Exercise #5

Identify which diagram shows the radius of a circle:

Step-by-Step Solution

Remember that a radius is a line segment connecting the center of the circle to a point that lies on the circle itself.

In drawing A, the line doesn't touch any point on the circle itself.

In drawing B, the line doesn't pass through the center of the circle.

We can see that in drawing C, the line that extends from the center of the circle is indeed connected to a point on the circle itself.

Answer:

Video Solution

Continue Your Math Journey

Master Tangent to a circle first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Circle Distance from a chord to the center of a circle Chords of a Circle Central Angle in a Circle Arcs in a Circle Perpendicular to a chord from the center of a circle Inscribed angle in a circle Circuit Components Elements of the circumference Area of a circle The Circumference of a Circle How is the radius calculated using its circumference?

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Calculate the ratio between radii of two circles Calculating arc length Calculating parts of the circle Identifying and defining elements