A circle has the equation: $$ x^2-6x+y^2-4y=7 $$ Use the completing the square method to find the center of the circle and its radius.

$$ (3,2),\hspace{6pt} R=\sqrt{20} $$

$$ (3,-2),\hspace{6pt} R=\sqrt{20} $$

A circle has the following equation: $ x^2-8ax+y^2+10ay=-5a^2 $ Point O is its center and is in the second quadrant ($$ a\neq0 $$) Use the completing the square method to find the center of the circle and its radius in terms of $$ a $$.

$$ O(4a,-5a),\hspace{4pt}R=-6a $$

$$ O(4a,5a),\hspace{4pt}R=6a $$

$$ O(4a,10a),\hspace{4pt}R=6a $$

$$ O(4a,-5a),\hspace{4pt}R=6a $$

Inscribed Angle Practice Problems & Solutions | Circle Geometry

Master inscribed angles in circles with step-by-step practice problems. Learn key properties, theorems, and relationships with central angles through guided exercises.

📚Master Inscribed Angles with Interactive Practice Problems

Identify inscribed angles with vertex on circumference and chord endpoints
Apply the inscribed angle theorem: inscribed angle equals half the central angle
Solve problems using equal inscribed angles that subtend the same arc
Calculate angles inscribed in semicircles that always measure 90 degrees
Find complementary inscribed angles on opposite sides of the same chord
Determine equal chords and arcs from equal inscribed angle relationships

Understanding Inscribed angle in a circle

Complete explanation with examples

Inscribed angle in a circle

An inscribed angle in a circle is an angle whose vertex is on the top of the circle (on the circumference of the circle) and whose ends are chords in a circle.

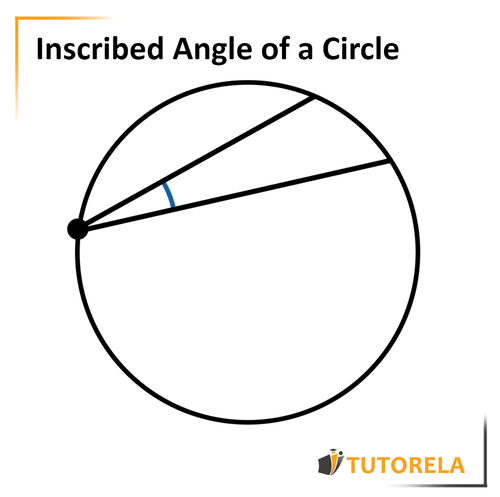
Therefore, if you draw any two chords in a circle, they will meet at the same point on the circumference - On the circle itself, we will create an angle.
The angle that will be formed, will be an inscribed angle in the circle.

Key Properties:

Inscribed angles that subtend the same arc from the same side are equal to each other.

Equal inscribed angles stand opposite equal chords and equal arcs.

An inscribed angle measures half the angle of the central angle that subtends the same arc.

Angles inscribed in semicircles always measure 90°, creating a right angle.

When two inscribed angles lean on the same chord but from opposite sides, their measures add up to $180°$

Detailed explanation

Practice Inscribed angle in a circle

Test your knowledge with 6 quizzes

Calculate the length of the arc marked in red given that the circumference is 12.

Examples with solutions for Inscribed angle in a circle

Step-by-step solutions included

Exercise #1

A point whose distance from the center of the circle is _______ than the radius, is outside the circle.

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is greater than the center of the circle will necessarily be outside the circle.

Answer:

greater

Exercise #2

Where does a point need to be so that its distance from the center of the circle is the shortest?

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is less than the radius from the center of the circle will necessarily be inside the circle.

Answer:

Inside

Exercise #3

In which of the circles is the point marked inside of the circle and not on the circumference?

Step-by-Step Solution

Let's remember that the circular line draws the shape of the circle, and the inner part is called a disk.

Therefore, in diagram B, the point is located in the inner part, meaning inside the disk.

Answer:

Video Solution

Exercise #4

Identify which diagram shows the radius of a circle:

Step-by-Step Solution

Remember that a radius is a line segment connecting the center of the circle to a point that lies on the circle itself.

In drawing A, the line doesn't touch any point on the circle itself.

In drawing B, the line doesn't pass through the center of the circle.

We can see that in drawing C, the line that extends from the center of the circle is indeed connected to a point on the circle itself.

Answer:

Video Solution

Exercise #5

Identify which diagram shows the radius of a circle:

Step-by-Step Solution

Remember that a radius is a line segment connecting the center of a circle to any point on the circle itself.

In drawing C we can see that the line coming from the center of the circle indeed connects to a point on the circle itself, while in the other drawings the lines don't touch any point on the circle.

Therefore, C is the correct drawing.

Answer:

Frequently Asked Questions

Everything you need to know about Inscribed angle in a circle

What is an inscribed angle in a circle?

An inscribed angle is an angle whose vertex lies on the circumference of a circle and whose two sides are chords of the circle. The vertex must be on the circle itself, not inside or outside it.

How do you find an inscribed angle when given the central angle?

The inscribed angle theorem states that an inscribed angle is always half the measure of the central angle that subtends the same arc. Simply divide the central angle by 2 to find the inscribed angle.

Why are inscribed angles in semicircles always 90 degrees?

When an inscribed angle subtends a semicircle (180° arc), it measures half of that arc according to the inscribed angle theorem. Half of 180° equals 90°, creating a right angle every time.

What happens when two inscribed angles subtend the same arc?

Inscribed angles that subtend the same arc from the same side of the circle are always equal to each other. This is one of the fundamental properties of inscribed angles in circle geometry.

How do inscribed angles on opposite sides of a chord relate?

When two inscribed angles subtend the same chord but from opposite sides of the circle, their measures always add up to 180°. They form supplementary angles.

What are the key properties of inscribed angles to remember?

Key properties include: 1) Inscribed angle = ½ central angle (same arc), 2) Equal inscribed angles subtend equal arcs, 3) Angles in semicircles = 90°, 4) Same-side inscribed angles are equal, 5) Opposite-side inscribed angles sum to 180°.

How do you solve inscribed angle problems step by step?

First, identify the inscribed angle and its arc. Then apply the relevant theorem: use the half-central-angle rule, equal arc property, or 90° semicircle rule. Finally, set up equations and solve algebraically if variables are involved.

What's the difference between inscribed and central angles?

A central angle has its vertex at the center of the circle with radii as sides, while an inscribed angle has its vertex on the circumference with chords as sides. The inscribed angle is always half the central angle subtending the same arc.

Continue Your Math Journey

Master Inscribed angle in a circle first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Circle Distance from a chord to the center of a circle Chords of a Circle Central Angle in a Circle Arcs in a Circle Perpendicular to a chord from the center of a circle Tangent to a circle Circuit Components Elements of the circumference Area of a circle The Circumference of a Circle How is the radius calculated using its circumference?

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Calculate the ratio between radii of two circles Identifying and defining elements Calculating arc length Calculating parts of the circle