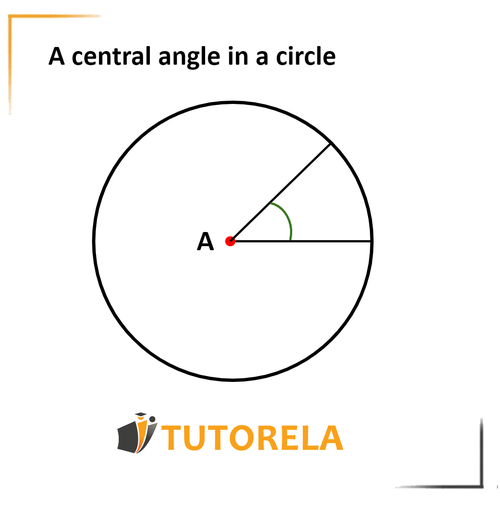
We are here to define what a central angle in a circle is and give you tips to remember its definition and properties in the best and most logical way.
Before talking about the central angle in a circle, let's take a moment to look at its name - a central angle.
Through its name, we can recognize that it has some connection with the center of the circle.
Great, now let's move on to the definition of a central angle and it will make much more sense to us.
Calculate the length of the arc marked in red given that the circumference is 12.
A point whose distance from the center of the circle is _______ than the radius, is outside the circle.
Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.
Therefore, a point whose distance is greater than the center of the circle will necessarily be outside the circle.
Answer:
greater
Where does a point need to be so that its distance from the center of the circle is the shortest?
Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.
Therefore, a point whose distance is less than the radius from the center of the circle will necessarily be inside the circle.
Answer:
Inside
In which of the circles is the point marked inside of the circle and not on the circumference?
Let's remember that the circular line draws the shape of the circle, and the inner part is called a disk.
Therefore, in diagram B, the point is located in the inner part, meaning inside the disk.
Answer:
Identify which diagram shows the radius of a circle:
Remember that a radius is a line segment connecting the center of a circle to any point on the circle itself.
In drawing C we can see that the line coming from the center of the circle indeed connects to a point on the circle itself, while in the other drawings the lines don't touch any point on the circle.
Therefore, C is the correct drawing.
Answer:
Identify which diagram shows the radius of a circle:
Remember that a radius is a line segment connecting the center of the circle to a point that lies on the circle itself.
In drawing A, the line doesn't touch any point on the circle itself.
In drawing B, the line doesn't pass through the center of the circle.
We can see that in drawing C, the line that extends from the center of the circle is indeed connected to a point on the circle itself.
Answer: