The formula for the sum of squares

$(X + Y)2=X2+ 2XY + Y2$

This formula is one of the shortcut formulas and it describes the square sum of two numbers.

That is, when we encounter two numbers with a plus sign (sum) and they are between parentheses and raised as an expression to the square, we can use this formula.
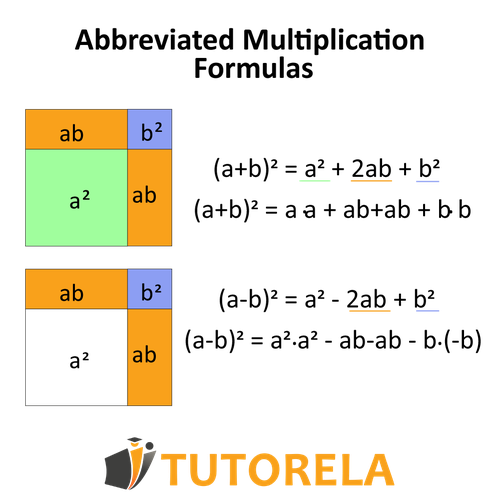
Pay attention - The formula also works for non-algebraic expressions or combined combinations with numbers and unknowns.
It's good to know that it is very similar to the formula for the difference of squares and differs only in the minus sign of the central element.

Detailed explanation

Start practice

Test yourself on square of sum!

Choose the expression that has the same value as the following:

$$ (x+y)^2 $$

Practice more now

Let's look at an example

$(X+9)^2=$
Here we identify two elements between which is the plus sign and they are within parentheses and raised to the square as a single expression.
Therefore, we can use the formula for the sum of squares.
We will work according to the formula and pay attention to the minus and plus signs.
We obtain:
$(X+9)^2=x^2+18x+81$
Indeed, we pronounce the same expression differently using the formula.

If you are interested in this article, you might also be interested in the following articles:

Square

The area of a square

Multiplication of the sum of two elements by the difference between them

The formula for the difference of squares

The formulas that refer to two expressions to the power of 3

In the blog of Tutorela you will find a variety of articles about mathematics.

Examples and exercises with solutions for the formula for the sum of squares

Exercise #1

Choose the expression that has the same value as the following:

$(x+3)^2$

Video Solution

Step-by-Step Solution

We use the abbreviated multiplication formula:

$x^2+2\times x\times3+3^2=$

$x^2+6x+9$

Answer

$x^2+6x+9$

Exercise #2

$(7+x)(7+x)=\text{?}$

Video Solution

Step-by-Step Solution

According to the shortened multiplication formula:

Since 7 and X appear twice, we raise both terms to the power:

$(7+x)^2$

Answer

$(7+x)^2$

Exercise #3

$4x^2+20x+25=$

Video Solution

Step-by-Step Solution

In this task, we are asked to simplify the formula using the abbreviated multiplication formulas.

Let's take a look at the formulas:

$(x-y)^2=x^2-2xy+y^2$

$(x+y)^2=x^2+2xy+y^2$

$(x+y)\times(x-y)=x^2-y^2$

Taking into account that in the given exercise there is only addition operation, the appropriate formula is the second one:

Now let us consider, what number when multiplied by itself will equal 4 and what number when multiplied by itself will equal 25?

The answers are respectively 2 and 5:

We insert these into the formula:

$(2x+5)^2=$

$(2x+5)(2x+5)=$

$2x\times2x+2x\times5+2x\times5+5\times5=$

$4x^2+20x+25$

That means our solution is correct.

Answer

$(2x+5)^2$

Exercise #4

$(2\lbrack x+3\rbrack)^2=$

Video Solution

Step-by-Step Solution

We will first solve the exercise by opening the inner brackets:

(2[x+3])²

(2x+6)²

We will then use the shortcut multiplication formula:

(X+Y)²=X²+2XY+Y²

(2x+6)² = 2x² + 2x*6*2 + 6² = 2x+24x+36

Answer

$4x^2+24x+36$

Exercise #5

$(x+1)^2+(x+2)^2=$

Video Solution

Step-by-Step Solution

In order to solve the exercise, we will need to know the abbreviated multiplication formula:

In this exercise, we will use the formula twice:

$(x+1)^2=x^2+2x+1$

$(x+2)^2=x^2+4x+4$

Now, we add:

$x^2+2x+1+x^2+4x+4=2x^2+6x+5$

x²+2x+1+x²+4x+4=
2x²+6x+5

Note that a common factor can be extracted from part of the digits: $2(x^2+3x)+5$

Answer

$2(x^2+3x)+5$

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Choose the expression that has the same value as the following:

$$ (x+3)^2 $$

Question 2

$$ 4x^2+20x+25= $$

Question 3

$$ (x^2+4)^2= $$

Start practice