Factorization

We will use the abbreviated multiplication formulas to convert expressions with terms that have addition or subtraction signs between them into expressions whose terms are multiplied.

$a^2-b^2=(a-b)\cdot(a+b)$

$a^2+2ab+b^2=(a+b)^2$

$a^2-2ab+b^2=(a-b)^2$

To use the first formula:
$a^2-b^2=(a-b)\cdot(a+b)$

We will ask ourselves:

• Is there a positive expression and another negative one?
• Can we find the root of each of the expressions separately?

If we have answered affirmatively to both questions, all that remains for us to do is simply take the root of the two terms and write them according to the formula.

Observe:

• We will place the roots within the parentheses.
• In case there are two positive terms or two negative terms, it will not be possible to use this formula.

To use the other formulas:
$a^2+2ab+b^2=(a+b)^2$

$a^2-2ab+b^2=(a-b)^2$

We must verify that three conditions are met.

We will ask ourselves:

• Do the two terms from which we will take the roots have the same sign? That is, are both positive or both negative?
• Can we take the root of the two terms separately?$a$  and $b$ ?
• If we multiply the product of the roots by $2$ will we obtain the middle term (in positive or in negative)?

If all the answers are affirmative, all that remains for us to do is simply place the obtained roots in the corresponding formula. Note that, if the middle term was negative in the original exercise, we will place it in the formula with the subtraction sign.

When can these formulas not be used?

When in the original exercise the signs of the terms from which we want to take roots are different, that is, one positive and the other negative, we will not be able to use these formulas.

We can remove a factor that is common to both elements from the parentheses and leave inside a simple and comfortable expression.
The common factor is the greatest factor that is completely common to both elements.

Notice which is the largest free number we can extract.

Then let's move on to the variables and ask

What is the least number of times the $X$ appears in any element?

Multiply the free number by the variable the number of times we have found and we will obtain the greatest common factor.

Extracting the common factor is the first operation we try to carry out when we need to break down some expression into factors.

To verify that you have extracted the common factor correctly, open the parentheses and see if you have arrived at the original exercise.

We introduce you to the trinomial:
$ax^2+bx+c$

The trinomial represents an expression in which the $X$ is raised to the second power and is preceded by a coefficient that can be positive or negative, but never $0$ (sometimes the coefficient is equal to $1$ and, in those cases, the a is not seen), to this element another $bx$ can be added or removed, where the $b$ represents the coefficient (under the same conditions as the a) and an independent variable -number-> $c$ can be attached. It doesn't matter if the coefficients of the variables are positive or negative, as long as they are according to the trinomial model, the exercise will be called a trinomial.

The factorization will look as follows:
 (x+solution\space one)(x+solution\spacetwo)

We will look for two numbers whose product is $a\cdot c$ and whose sum is $b$

We will ask ourselves: which number multiplied by which other will give us $a\cdot c$ or $​​c$ (if $a$ equals $1$).
and what plus what will add up to $b$.

In fact, we have to find a pair of numbers that meet these two conditions at the same time.

We can plot it as follows:

Course of action:
We will find all the numbers whose products are $A\cdot C$ and write them down.
Then, we will see which pair of numbers among those we found will result in $B$.
The two numbers that meet both conditions are the solutions to the trinomial.

Important:

• If A were different from $1$ it would appear before the parentheses and then there would be a multiplication.
• If any of the solutions or both were negative we would not add them to the $X$ but subtract them.

$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$

$a$ The coefficient of the first term
$b$ The coefficient of the second term
$c$ The constant term

In the first step, we will use only the addition to find the first solution, and then, we will use only the subtraction to find the second.
Again, the factorization will look as follows:
$(x+first\space solution)(x+second\space solution)$
or with subtractions, depending on the results.

Algebraic fractions are fractions with variables.
Methods for factoring algebraic fractions:

• We will find the most suitable common factor to extract.
• If we do not see a common factor that we can extract, we will proceed to factorization with formulas for shortcut multiplication, as we have studied.
• If shortcut multiplication formulas cannot be used, we will proceed to factorize with trinomials.
• We will reduce according to the rules of reduction (multiplication of elements).

Note, you can factorize every expression included in your fraction in any way you wish and, in the end, you will arrive at factorized expressions.

To add or subtract algebraic fractions, we must make all the denominators the same, that is, find the common denominator.

To do this, we will factorize according to the different methods we have learned.

Action steps:

• We will factorize all the denominators we have.
• We will note the common denominator.
• We will multiply each of the numerators by the same number that we need to multiply its denominator in order to reach the common denominator.
• We will write the exercise with a single denominator, the common denominator, and among the numerators, we will keep the same mathematical operations that were in the original exercise.
• After opening the parentheses, it may happen that we encounter another expression that needs to be factorized. We will factorize it and see if we can simplify it.
• We will obtain a common fraction and solve it.

You can simplify algebraic fractions only when there are multiplication operations among the elements of the numerator.
Note that, if there are additions or subtractions among elements enclosed in parentheses, we can simplify since these are considered as a single element.

In any other case, it cannot be simplified.
After factoring, you will be able to simplify these fractions very easily.
Steps to simplify fractions:

• Observe the following exercise and try to understand it.
• Try to find the common factor.
• Try to simplify using the formulas for abbreviated multiplication.
• Attempt to factorize with trinomials.

Action steps for multiplying algebraic fractions:

• Let's try to extract the common factor.

This can be the variable or any free number.

• If this is not enough, we will factorize using shortcut multiplication formulas and trinomials.
• Let's find the solution set.

How is the solution set found?
We will make all the denominators we have equal to $0$ and find the solution.
The solution set will be $X$: different from what causes our denominator to equal zero.

• Let's simplify the fractions safely.
• Multiply numerator by numerator and denominator by denominator as in any fraction.

Action Steps for Dividing Algebraic Fractions:

• We will convert the division exercise into a multiplication one, just as we do with common fractions.

How will we do it correctly?

We will leave the first fraction as it is, change the division sign to a multiplication sign, and invert the fraction that comes after the sign. That is, numerator in place of denominator and denominator in place of numerator.

• We will act according to the rules of multiplying algebraic fractions:

1. We will try to extract the common factor.

This can be the variable or any free number.

1. If this is not enough, we will factorize using formulas for short multiplication or with trinomials.
2. We will find the solution set.

• How is the solution set found?

We will make all the denominators we have equal to $0$ and find the solution.

The solution set will be: $X$ different from what causes our denominator to equal zero.

• Let's simplify the fractions safely.
• Multiply numerator by numerator and denominator by denominator as in any fraction.

Solving Equations by Factoring
Let's remember the rule:

The product of two numbers equals $0$ when at least one of them is $0$.

If $x\cdot y=0$
then
either: $x=0$
or: $y=0$
or both are $0$.
Action steps to solve equations by factoring:

1. Let's move all the elements to one side of the equation and leave $0$ on the other.
2. Let's factor using one of the methods we have learned: by taking out the common factor, with shortcut multiplication formulas, or with trinomials.
3. Let's see when the elements reach a product equivalent to $0$.

Factorization is an algebraic method that you will apply, automatically, in most of the exercises you will receive from now on.

Factorization allows us to represent and convert terms between which there are additions or subtractions to terms with multiplication or division operations.

When correctly factorized, the result does not change, only that the exercise is represented in a different way.

Clearly, we are not talking only about modifications in the operations of addition and subtraction to those of multiplication and division, but about a radical change that applies to all the factors involved.

Why would we want to factorize?

You might be wondering why on earth we would want to convert terms with additions and subtractions into others with multiplications and divisions.

If so, it's important for you to know that factorization is the main key to solving more complex exercises than those you have solved up to now.

After reading everything explained here, you will know how to factorize with total confidence, in all ways, easily and quickly.

This way, you will be able to solve the exercises you receive without any problem.

Wait... How will you know if it's convenient to factorize?

Here we will list the main uses of factorization.

1.When you come across exercises where the sum or difference of their terms equals zero, it will be convenient for you to apply the technique of factorization.

By factorizing, we convert the sum and subtraction into multiplication and division operations.

With the technique of factorization, we can convert the total or the difference into a product and, it is known that, if the product equals $0$ it means that at least one of the terms among which there are multiplication signs must be $0$

(since it causes the product to be equivalent to zero).

For example:

given an exercise like this:
$x^2+8x+15=$

An exercise that, at this moment, seems terrifying and too challenging, we can observe and understand that we can apply the technique of factorization.

All terms are on one side and on the second there is nothing, that is $0$.

Among the terms there are sums.

Therefore, with the technique of factorization, which we will learn right now, we can represent this exercise in the following way:
$(x+3)\cdot(x+5)=0$

It looks much simpler now, right?

We see that there are two expressions whose product equals $0$.

We can determine that the first expression equals zero and then $x=-3$
or that the second expression equals zero and then $x=-5$
or both. Consequently, the results will be $x=-3,-5$

2.When you come across fractions that have complicated expressions like the previous example, you can arrive at much simpler fractions with the correct factorization and simplification of the elements.

We have said that, with the help of factorization we represent the exercise that has operations of sum and subtraction as one with multiplication and division operations, this means that we do not modify the exercise itself, only its representation.

Then, we can factorize and simplify the exercise in the way that is most comfortable for us to arrive at the correct result.

For example, given an exercise like this:
$\frac{3X^2-14X+8}{3X^2+X-2}=$

At first glance, it would seem that we cannot simplify the exercise and arrive at a simpler fraction since we cannot do it when the expression is composed of sum and subtraction operations.

But hey! Precisely for this, we will learn the technique of factorization.

Thanks to a simple factorization we can obtain the same exercise, but in the following form:

$\frac{(X-4)\cdot(X-\frac{2}{3})}{(X-\frac{2}{3})\cdot(X+1)}=$

Pay attention!

Now we can easily simplify the term $X-\frac{2}{3}$
We will simplify and obtain:

$\frac{X-4}{X+1}$

From a quite complicated expression, we arrive at a simple expression by applying factorization.

Great... Now that you understand how much factorization can help you in solving exercises, you must surely be curious and want to learn the best techniques for successful factorization.

Don't worry, that's exactly what we're here for.

We will teach you step by step all the ways for efficient factorization.

Let's start with the first one.

Factorization according to short multiplication formulas

You have surely come across the short multiplication formulas at some point.

The short multiplication formulas will help you convert expressions with terms that had multiplication operations between them into expressions whose terms are added or subtracted.

As we have mentioned before, factorization does exactly the opposite.

It converts expressions with terms that have plus or minus signs between them into expressions whose terms are multiplied or divided.

As a result, we will be able to use the short multiplication formulas we know and rotate them in favor of factorization.

Let's start by remembering the short multiplication formulas:
$(a-b)\cdot(a+b)=a^2-b^2$

$(a+b)^2=a^2+2ab+b^2$

$(a-b)^2=a^2-2ab+b^2$

The formulas helped us open the parentheses and see the expressions without them.

Now we will learn how to factorize and enclose the terms within the parentheses again.

Let's start with the first formula, this time we will rotate the expressions to make it more comfortable for us to understand:
$a^2-b^2=(a-b)\cdot(a+b)$

As you can see, it involves two terms raised to the power of two, which have a subtraction operation between them.

In fact, we are talking about a positive term and a negative term, both squared, each one separately.

Let's see an example:
$x^2-16=$
How will we know if it will be possible to solve the exercise with the formula we saw above?

We will ask ourselves:

• Is there a positive expression and a negative one? The answer is yes.
• Can we find the root of each of the expressions separately? The answer is yes.

Perfect! Now, all that remains for us to do is simply take the root of these two terms.

If we take the root of the first term we will obtain $X$.

If we take the root of the second term we will obtain $4$.

Now we will write the roots we obtained according to the formula:
$x^2-16=(x-4)\cdot(x+4)$

Observe, according to the formula $B$ is $4$.

Since $16=4^2$

So, indeed, if we see two terms from which we can extract the root and one is positive and the other negative, we can apply the first multiplication formula easily.

Attention! Observe the exercise very carefully and locate the roots within the parentheses. If in the previous exercise we had placed the $16$ inside the parentheses and had not extracted the root, we would have obtained a wrong answer.

And what would happen in case there was an exercise like this:
$-x^2+25$

We will act with the same system:

• Is there a positive expression and another negative one? The answer is yes.
• Can we find the root of each of the expressions separately? The answer is yes.

Therefore, clearly, we can apply the abbreviated multiplication formula.

The operation of adding between the elements does not imply that we cannot use this formula.

The change in this exercise is only the order in which its elements are written.

We can still see that we can extract roots from the third and fourth element.

To avoid confusion we will turn the exercise to its correct mode and we will obtain:
$25-x^2=$
The factorization will look like this:
$(5-x)\cdot(5+x)$

Observe - In case there are two positive terms or two negative terms, we cannot use this formula.

Now we will move on to the next two abbreviated multiplication formulas and we will turn them to understand them better:

$a^2+2ab+b^2=(a+b)^2$

$a^2-2ab+b^2=(a-b)^2$

Those with a keen eye will probably notice that these two formulas are almost identical, and that the only difference between them is the sign between the elements or the one preceding the $2ab$.

As we can see, there are two terms $A$ and $B$ from which a root can be extracted. In addition, the product of the elements by $2$ is added or subtracted.

Let's see an example:
$x^2+12x+36=$

How will we know if it will be possible to solve the exercise with the formula we saw above?

We must verify three conditions. We will ask ourselves:

• Do the two terms from which we will extract the roots have the same sign? That is, are both positive or both negative?

The answer is yes.
$36$ Positive and $x^2$ positive.

• Can we extract the root of the two terms separately? $a$ and $b$?
  The answer is yes.
  The roots of term $a$ are $x$

and the root of $b$ is $6$.

• Does the product of the roots by $2$ give the middle term (in positive or negative)?

The answer is yes.

If we multiply term $a$

by term $b$ and $2$,

we will obtain the middle term:
$x\cdot6\cdot2=12x$

Perfect! Now, all that remains for us to do is simply place the obtained roots in the corresponding formula:
$(x+6)^2$
Observe, if the middle term were negative in the exercise, that is:
$x^2-12x+36=$
we would have used the other formula and the factorization would look like this:
$(x-6)^2$

Let's see an example of using the formula with the subtraction sign:
$x^2-6x+9$
Again, we must verify that three conditions are met. We will ask ourselves:

• Do the two terms from which we will extract the roots have the same sign? The answer is yes. Both are positive.
• Can we extract the root of the two terms separately? $A$ and $B$? The answer is yes.

The root of term $A$ is $X$ and the root of term $B$ is $3$.

• Does the product of the roots by $2$ give the middle term (in positive or negative)? The answer is yes.

If we multiply term $A$ by term $B$ and by $2$ we will obtain the middle term:
$x\cdot3\cdot2=6x$

Observe, the middle term in the original exercise is $-6x$ and we have obtained $6x$.

Therefore, we will use the formula with the subtraction sign and we will obtain:
$(x-3)^2$

When can these formulas not be used?

When in the original exercise the signs of the terms from which we want to extract roots are different, that is, one positive and one negative, we cannot use these formulas.

Factorization by taking the common term out of the parentheses

Sometimes, we can take out of the parentheses a factor that is common to both elements and leave inside a simple and comfortable expression.

What does common factor mean?

The common factor is the greatest factor that is completely common to both elements.

For example, in the following exercise:
$3x+21=$
Separating each element of the exercise we will obtain:
$3\cdot x+3\cdot7=$
We will see that the common factor to both expressions is $-3$.
Therefore, in the following way we can extract it from the expression using parentheses, and we will obtain exactly the same expression seen in another way:
$3(x+7)$
If we open the parentheses we will clearly obtain:
$3x+21=$

What we have done is remove the greatest common factor to both elements. From $3x$ we took out $3$

and it left$x$ and from $21$ we took out $3$ and it left $7$.

We can extract any factor as a common factor, even unknowns and unknowns with coefficients.

Let's see it in the following exercise:
$4x^2+8x=$
By disassembling the expression we will obtain:
$4\cdot x\cdot x+8\cdot x=$
The greatest common factor that we can extract is $4x$
We will be left with:
$4x(x+2)=$
The more you practice the way of extracting the common factor, the more intuitive it will become.
Our suggestion:

First, find the greatest free number you can extract.

In the previous example, let's look at the free numbers and ask, what is the greatest factor by which $4$ and $8$ divide without a problem?

The answer is $4$.

Then, we will move on to the unknowns and ask what is the minimum amount of times that the $X$ appears in a particular element?

The answer is once.

Then we can extract $4\cdot X$.
When is it necessary to extract the common factor?
Let's repeat, as in the beginning of factorization with the abbreviated multiplication formulas, the extraction of the common factor helps us to factorize and to solve the exercise correctly and efficiently.

In cases where there is a difference or total equivalent to $0$, we can convert the exercise to a product and examine when the factors reach zero.

Also, in fractions, we can extract a common factor and thus easily reduce the fraction.

Let's see an example:
$x^3-x^2=0$
We will want to extract the common factor.

We will ask ourselves What is the greatest common factor that we can take out of the two terms? The answer is $x^2$

if we take out $x^2$ from $x^3$, we will be left with $x$ and if we take out $x^2$ from $-x^2$ we will be left with $-1$.
Consequently, the expression will look like this:
$x^2 (x-1)=0$

Now, we can solve it easily.

We will ask ourselves When does the expression equal zero?

Since here there are factors or $x^2$ equals $0$ or $(x-1)$ equals $0$.
We will solve and obtain:
Case 1:

$​​​​​​​x^2=0$
$x=0$
Case 2:
$​​​​​​​x-1=0$
$x=1$

Therefore, the results will be:
$x=0,-1$

Do you want to check that you have extracted the common factor correctly?

No problem. Simply open the parentheses and see if you arrive at the original exercise.

If the answer is yes, it means you have extracted the common factor correctly. If not, you have made a mistake and must try again.

Factorization of Trinomials

Don't be scared of the term trinomial. Think of it as a tool you can use to break down your exercise into factors.

Let's introduce the trinomial:
$ax^2+bx+c$

The trinomial represents an exercise in which the $x$ is squared, preceded by a coefficient, positive or negative, but never $0$ (sometimes the coefficient is equal to $1$ and therefore we won't see the $a$,) to this term may be added or subtracted some other $bx$, when $b$ represents the coefficient (under the same conditions as $a$) and the independent variable - number $c$ that is not $0$ is added or subtracted.

In fact, the trinomial could look like this: $ax^2-bx-c$

Regardless of whether the coefficients of the terms are positive or negative, as long as they appear in the form of a trinomial, the exercise will be called "trinomial".

Trinomial model:

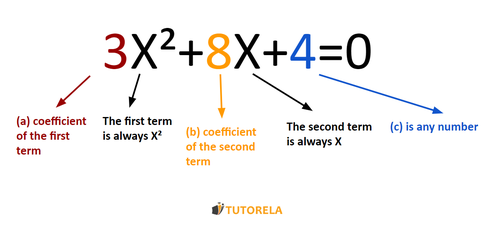
The factorization will look like this:
$(x+First\space Solution)(x+Second\space Solution)$
or with subtractions, depending on the results.

Let's see an example and try to understand exactly the values of these parameters: $x^2+4x+5=$

$a$ The coefficient of the first element is $1$. Notice, it's not $0$. Even though you don't see it, it exists and it's $1$. If it had been $0$, the first term would have also turned into zero. Instead, multiplying by $1$ does not change the term.
$b$ The coefficient of the second element is $4$.
$c$ The free number is $5$.

Now we will learn how to factorize with trinomials. We will teach you two main ways.

Attention: we recommend doing it this way only when the coefficient of $a$ is equal to $1$.

When looking at our trinomial, we will try to find two numbers whose product is $a\cdot c$ and their sum is $b$.
Indeed, we will ask: which number multiplied by which other will give us $ac$ or $c$ (if $a$ is equal to $1$)
(and, which number plus which other will add up to $b$.
Indeed, we have to find a pair of numbers that meet these two conditions at the same time.
We can plot it as follows:

First, we will find all the numbers whose products are $AC$ and write them down.

Then, we will see which pair of numbers added together will give us $B$ as a result.

The two numbers that meet both conditions will be the solutions to the trinomial.

Let's see an example:

$x^2+7x+6=$

First, we will ask ourselves,

what number multiplied by which other will give us $6$?

$6, 1$
$2,3$

Note that, even if these numbers were negative their product would be $6$ (since negative times negative gives positive).

Therefore, we will also add:
$1-, 6-$
$​​$,$​​-3,-2$

and then, we will ask what the sum of which pair of numbers will give us $7$?

The answer is: $6, 1$

Then the factorization of the trinomial will be: $x^2+7x+6=(x+1)\cdot(x+6)$

Observe, if $a$ differed from $1$ it would appear before the parentheses and then there would be a multiplication.

Suggestion:
The first way is more timely for cases in which the coefficient of the first element $a$ is equal to $1$.
Then we can ask which are the two numbers whose product $c$ and their sum is $b$.

If $a$ differs from $1$, we will prefer to factorize in the second way.

Note: If any of the solutions or both were negative we would not add them to the $X$ but subtract them.

For example:
$x^2-7x+6=(x-1)\cdot(x-6)$

Do you want to verify that you have factored correctly? You can open the parentheses and see if you arrive at the original exercise.

If you are not the trial and error type, and prefer to arrive at a concrete answer even when $a$ differs from $1$ it is convenient to know the quadratic formula.

The quadratic formula:

$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$

We know it might look a bit scary at first glance, but trust us, you just need to identify the elements in your original exercise and substitute them into the formula.

Moreover, you're probably wondering what the plus and minus signs together mean.

The answer is simple.

Once we will only use the plus and find the first solution, and another time we will use only the minus and find the second solution.

The quadratic formula will help us solve any quadratic equation.

Let's solve the trinomial with this formula.

Let's take, for example, the trinomial:
$​​​​​​​x^2-8x+15=$

First step:

We will write down the values of all the parameters as we have learned:
$a=1$
$b=-8$
$c=15$

Now, we simply place them in the formula:
$=\frac{-(-8)±\sqrt{(-8^2)-4\cdot1\cdot15}}{2\cdot1}$

The first time we will solve only with the plus sign:

$=\frac{-(-8)+\sqrt{(-8^2)-4\cdot1\cdot15}}{2\cdot1}$

$=\frac{8+\sqrt{64-60}}{2}$

$=\frac{8+\sqrt{4}}{2}$

$=\frac{8+2}{2}=\frac{10}{2}=5$

$5$ is our first result.

Now we move on to the formula with the minus sign:
$=\frac{-(-8)-\sqrt{(-8^2)-4\cdot1\cdot15}}{2\cdot1}$

Notice that we can copy everything that was inside the square root and simply change the plus sign to a minus sign like this:
$=\frac{8-\sqrt{4}}{2}$
$=\frac{8-2}{2}=\frac{6}{2}=3$

Our second result is $3$.

Therefore, $x^2-8x+15=(x+5)\cdot(x+3)$

Practice both ways over and over to know how to correctly and efficiently factor trinomials.

Now, we will learn how to factor algebraic fractions.

Factorization of Algebraic Fractions

So, what are algebraic fractions?

Algebraic fractions are fractions with variables.

In fact, everything we have studied about factorization also makes sense in the factorization of algebraic fractions.

When we want to decompose algebraic factors, we will act in the following ways:

1. We will find the most suitable common factor to extract.

What does that mean?

The key in algebraic fractions is that they should be simplified, therefore, sometimes we will look for the common factor that suits us best to extract in order to reduce the fraction.

2. If we do not see a common factor that we can extract, we will move on to factorization with shortcut multiplication formulas, as we have studied.

The shortcut multiplication formulas also break down the expression into factors and help us reduce the fraction.

3. If the shortcut multiplication formulas cannot be used, we will proceed to factorize with trinomials.

Pay attention! You can factorize every expression included in your fraction in any way you want and, in the end, you will arrive at factorized expressions.

Let's see an example in which we will use various methods of factorizing algebraic fractions:

$\frac{x^2-8x+16}{x^2-4x}=$

We will notice that we can factorize the numerator through a trinomial and the denominator by extracting a simple common factor.

We will obtain:
$\frac{(x-4)(x-4)}{x(x-4)}=$
Now we can reduce the expression and obtain:
$\frac{x-4}{x}$

In fact, we have factorized each expression in the most suitable way for us.

In what other cases is factorization useful? When we want to add and subtract algebraic fractions.

Addition and Subtraction of Algebraic Fractions

To add or subtract algebraic fractions, we must make all the denominators the same, that is, find the common denominator.

To do this, we will need to factorize.

Action steps:

1. We will factorize all the denominators we have.
2. We will note the common denominator.
3. We will multiply each numerator by the necessary number to reach the common denominator.
4. We will write the exercise with a single denominator, the common denominator, and, among the expressions of the numerators, we will keep the same mathematical operations.
5. We will solve the fraction.

Let's see an example:

$\frac{x}{x+2}+\frac{3}{x+5}+\frac{6}{x^2+7x+10}=$

We have an exercise with the addition of several expressions. To add these fractions, we must make them have a common denominator.

How do we find the common denominator for all the fractions?

We will factorize the denominator of each fraction separately according to the different methods we have learned.

We see that, in this exercise, we only need to factorize the denominator of the third element. We will do it with a trinomial.

And we will obtain:
$\frac{x}{x+2}+\frac{3}{x+5}+\frac{6}{(x+2)(x+5)}=$

The common denominator is $(x+2)(x+5)$. Therefore, we will draw a fraction line and write it:

Now, we must multiply each numerator by what it needs to reach the common denominator:

We will illustrate it in the following way so you can see it clearly:

We will obtain:
$\frac{x(x+5)+3(x+2)+6}{(x+2)(x+5)}=$

We will take care to keep the mathematical operations that are between the numerators.

We will open parentheses (without touching the common denominator) and we will obtain:
$\frac{x^2+5x+3x+6+6}{(x+2)(x+5)}=$
We will place the elements and it will give us:
$\frac{x^2+8x+12}{(x+2)(x+5)}=$
Pay attention! We have a trinomial in the numerator.

Luckily, we already know how to factorize it.

When we factorize, we will get:
$\frac{(x+5)(x+6)}{(x+2)(x+5)}=$

Oh... Now we can reduce the expression $x+2$

We will do it and we will obtain:
$\frac{x+6}{x+5}$
This is the final result!

Simplification of Algebraic Fractions

The simplification of algebraic fractions essentially sums up everything we have learned so far about factorization.

To simplify algebraic fractions effectively and correctly, you will need to know all the ways of factorization.

From extracting the common factor, through the formulas of abbreviated multiplication, to the factorization of trinomials.

Observe:

You can simplify algebraic fractions only when there are multiplication operations among the elements of the numerator.

However, if there are addition or subtraction operations in elements located between parentheses, we can also simplify since these are considered a single element.

In any other case, it cannot be simplified.

As we have already mentioned, factorization is the way to convert an exercise with addition or subtraction into one with multiplication.

After factorizing, you will be able to simplify these fractions very easily.

Steps to simplify fractions:

Observe the following exercise and try to understand it.

1. Try to find the common factor.
2. Try to simplify using the formulas of abbreviated multiplication.
3. Attempt to factorize with trinomials.

In some cases, you might come across a fraction that has opposite signs in the numerator and denominator.

For example:
$\frac{2x-1}{1-2x}$

Notice that you cannot simplify the expression because there is no multiplication operation between the elements (and also because the signs are different).

To reduce this fraction we must take out $-1$ in the denominator or in the numerator and then we will obtain the same expression in the denominator and in the numerator and we can simplify.

Let's take out $-1$ in the numerator and it will give us:
$\frac{(-1)(-2x+1)}{(1-2x)}=$

Notice that indeed we have received the same expression in the denominator and in the numerator and we can only keep $-1$.

We can also write:

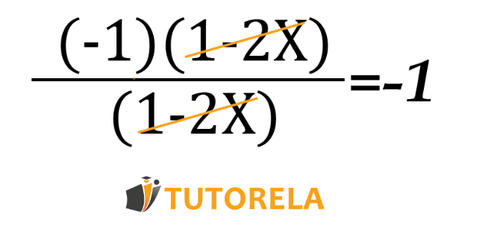
And thus see the simplification better. Notice that we have not modified the signs before the numbers.
$1$

Still positive and $-2x$ still negative.

Multiplication and Division of Algebraic Fractions

The multiplication and division of algebraic fractions is very similar to the multiplication and division of common fractions, so there's no need to stress.

The only difference between algebraic and common fractions is that we first need to factorize the given expressions.

Moreover, since it involves variables, we must find the solution set.

After doing so, we can simplify and discover the numerator and the multiplication.

First, let's try to find the common factor. The common factor can be our unknown or any free number.

If extracting the common factor is not enough, we will factorize using the formulas for short multiplication and also with the trinomial.

Then we will find the solution set.

How is the solution set found?

Let's observe our denominators and ask ourselves when they become zero.

That is, let's make them equivalent to $0$ and find the solutions.

The solution set will be: $X$ different from what causes the denominator to become zero.

Then, we can safely reduce the fractions and multiply numerator by numerator and denominator by denominator as in any common fraction.

Let's see an example:

$\frac{2x+4}{3x^2-3x}\cdot\frac{x-1}{4x^2+8x}=$

Let's factorize each expression through the ways we have learned:
$\frac{2(x+2)}{3x(x-1)}\cdot\frac{x-1}{4x(x+2)}=$

Let's find the solution set:

$3x(x-1)=0$
$x≠0,1$
$4x(x+2)=0$
$x≠0, -2$
Therefore, the solution set is:
$x≠0,1, -2$ Now, we can safely reduce the fractions.
We will reduce and obtain:

$\frac{2}{3x}\cdot\frac{1}{4x}=$
Let's multiply numerator by numerator, denominator by denominator and we will obtain:

$\frac{2}{12x^2}=\frac{1}{6x^2}$

Now let's move on to the division of algebraic fractions.

Division of Algebraic Fractions

When we have a division of algebraic fractions, we will first convert the division exercise into a multiplication one, just as we do with common fractions.

How will we do it correctly?

We will leave the first fraction as it is, change the division sign to a multiplication sign, and invert the fraction that appears after the sign. That is, the numerator becomes the denominator and vice versa.

Then, when the exercise becomes a multiplication exercise, we will solve it exactly as we have studied before. First, we will try to factorize by extracting the common factor, with the formulas for abbreviated multiplication and with trinomial,

we will find the solution set, reduce, and multiply numerator by numerator and denominator by denominator.

Let's see an example:
$\frac{x^2-10x+25}{x^2+2x}:\frac{x^2-25}{x+2}=$

Even before looking at the exercise, let's convert it into a multiplication exercise. We will leave the first fraction as it is, change the division sign to a multiplication sign, and invert the second fraction.

We will do it and obtain:
$\frac{x^2-10x+25}{x^2+2x}\cdot\frac{x+2}{x^2-25}=$

Great. Now we will act according to the rules of multiplication of algebraic fractions.

Let's factorize in all the ways we know:

$\frac{(x-5)(x-5)}{x(x+2)}\cdot\frac{x+2}{(x-5)(x+5)}=$

Let's find the solution sets:
$x≠0,-2,5,-5$
Let's reduce the fractions:

We will obtain:

$\frac{x-5}{x}\cdot\frac{1}{x+5}$

Let's multiply numerator by numerator and denominator by denominator, we will obtain:
$\frac{x-5}{x(x+5)}$

Solving Equations by Factoring

We can solve equations by breaking down factors easily and quickly if we strictly follow the appropriate steps.

The key lies in knowing all the ways to successfully factor and, of course, in understanding a basic mathematical rule.

The rule we are talking about is that the product of two terms equals zero if at least one of the terms is equal to $0$.

That is, given the equation $x\cdot y=0$
The equation will only be consistent if, at least, one of its terms is $0$.

Or:
$x=0$   or: $y=0$

Excellent. Once this rule is mentioned, let's continue with the desired order of operations for solving equations with factoring.

When you come across an equation, first you will have to move all the elements to one side and leave $0$ on the other.

For example, if you have an equation like this:
$x^2+8x=-2x$

You will have to transfer terms to leave only the $0$ on one of them.

Let's transfer terms and we will get: $x^2+8x+2x=0$

Now it's clearer that factoring will be very effective in an equation like this.

Since, in factoring, what we actually do is convert an expression that has additions or subtractions into another with multiplication operations and, as we have already mentioned, when the elements are multiplied and their product is $0$, it will be very easy to find the solutions.

So, after transferring terms and leaving the $0$ on one of them, we will try to factor the equation by extracting the common factor, formulas for abbreviated multiplication, or trinomial.

We will place elements in the equation from the previous example and obtain:

$x^2+10x=0$
Now, let's extract the common factor and we will get:
$x(x+10)=0$
We will ask ourselves when does the equation equal zero?

The answers are obviously:

when $x=0,-10$
these are our solutions.

Now that you know everything about factoring, all the ways to do it, and its uses, you can practice the methods over and over again and arrive at the exam very happy with excellent preparation!

If you are interested in this article, you might also be interested in the following articles:

• Factorization
• The uses of factorization
• Factorization according to short multiplication formulas
• Factorization through the extraction of the common factor outside the parentheses
• Factorization of trinomials
• Factorization of algebraic fractions
• Addition and subtraction of algebraic fractions
• Simplification of algebraic fractions
• Multiplication and division of algebraic fractions
• Solving equations through factorization

On the Tutorela blog, you will find a variety of articles about mathematics.