Which shapes are similar? 8 8 8 8 8 8 12 12 12 6 6 6 8 8 8 6 6 6 14 14 14 6 6 6 14 14 14 3.5 3.5 3.5 1.5 1.5 1.5 3.5 3.5 3.5 6 1.5

Only the two triangles are similar.

Which statement is true? <path d="m1129.063 183.974 331.704 132.682M1460.767 316.656l-66.34 331.704M1394.426 648.36l-398.044-66.341M996.382 582.019l132.681-398.045M133.951 183.974l597.067 66.341M731.018 250.315 598.337 714.701M598.337 714.7 67.61 582.02M67.61 582.019l66.341-398.045" fill="none" paint-order="fill stroke markers" stroke="#DB6114" stroke-linecap="round" stroke-linejoin="round" stroke-miterlimit="10" stroke-opacity=".8" stroke-width="2.5">

The polygons are similar and congruent.

Which statement is true for similar polygons?

The ratio between the lengths of the sides of two polygons is equal to the ratio between the perimeters of the two polygons.

The ratio between the lengths of the sides of two polygons is equal to the ratio between their areas.

The ratio between the lengths of the sides of two polygons is not equal to the ratio between the perimeters of the two polygons.

The ratio between the perimeters of two polygons is equal to the ratio between their areas.

The ratio between the lengths of the sides of two polygons is equal to the ratio between the perimeters of the two polygons.

Similarity of Geometric Figures

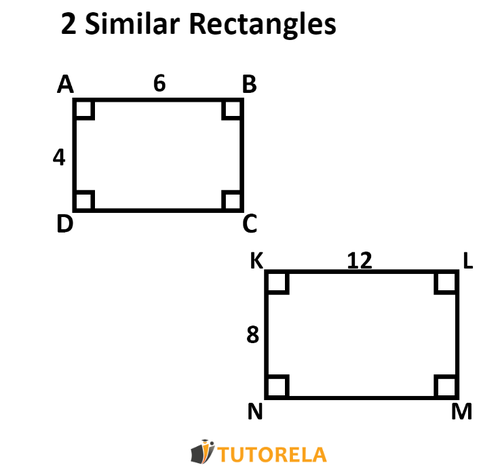
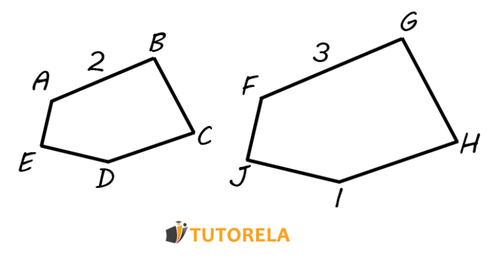
Similarity in geometry refers to the relationship between two shapes that have the same shape but may differ in size. Two figures are similar if their corresponding angles are equal and the lengths of their corresponding sides are proportional. This means one figure can be obtained by resizing the other, either by scaling up or scaling down, without changing the shape.

While similarity is most commonly associated with triangles, it can apply to almost any shape or figure.

Similar geometric have these key properties:

They have angles of the same size respectively. In other words, all corresponding angles between similar figures are equal, preserving the overall shape.
Proportionality between the sides of such figures - the ratios of corresponding side lengths are the same across similar figures.

In an intuitive way, just as it happens with triangles, two similar figures are, in fact, an enlargement of the other.

Detailed explanation

Start practice

Test yourself on similarity of polygons!

Is rectangle ABCD similar to rectangle EFGH?

Practice more now

Similarity of Geometric Figures

Example 1

Let's demonstrate this topic with an example.

We have an illustration of two similar rectangles, $ABCD$ and $KLMN$ .

In both rectangles all angles are right angles (equivalent to $90º$ ).

Moreover, each side of the large rectangle $KLMN$ is greater than the respective side in the small rectangle $ABCD$ .

That is, $KL=12$ in the large rectangle $KLMN$ is twice as long as $AB=6$ in the small rectangle $ABCD$ , and $KN=8$ in the large rectangle $KLMN$ is twice as long as $AB=4$ in the small rectangle $ABCD$ .

Example 2

These two squares are similar:

The two corresponding angles are equal since all angles are right angles. The ratio between the corresponding sides, that is, the scale factor is
$2:1$

or, in other words, each side of the larger square measures twice as much as each side of the small square

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

In front of you are two hexagons with a similarity ratio. Which angles are corresponding?

Question 2

Look at the two similar rectangles below and calculate the perimeter of the larger rectangle.

Question 3

The two parallelograms above are similar. The ratio between their sides is 3:4.

What is the ratio between the the areas of the parallelograms?

Example 3 - Similar Figures

The two pentagons in the illustration are similar, meaning, the corresponding angles are equal. The ratio of similarity is

$\frac{EF}{AB}=\frac{3}{2}=\frac{1.5}{1}$

That is, the length of each side in the pentagon $FGHIJ$ is $1.5$ times greater than that of its corresponding side in the pentagon $ABCDE$

If you are interested in this article, you might also be interested in the following articles

In the blog of Tutorela you will find a wide variety of mathematics articles

Examples and exercises with solutions on similarity of geometric figures

Exercise #1

Look at the two similar rectangles below and calculate the perimeter of the larger rectangle.

Video Solution

Step-by-Step Solution

Let's remember that in a rectangle there are two pairs of parallel and equal sides.

We will call the small triangle 1 and the large triangle 2.

We calculate the perimeter of the small triangle:

$P_1=2\times3.5+2\times1.5=10$ Since we know that the rectangles are similar:

$\frac{3.5}{14}=\frac{p_1}{p_2}$

We place the data we know for the perimeter:

$\frac{3.5}{14}=\frac{10}{p_2}$

$\frac{3.5}{14}\times p_{_2}=10$

$p_2=10\times\frac{14}{3.5}$

$P_2=40$

Answer

40 cm

Exercise #2

The two parallelograms above are similar. The ratio between their sides is 3:4.

What is the ratio between the the areas of the parallelograms?

Video Solution

Step-by-Step Solution

The square of the ratio between the sides is equal to the ratio between the areas of the parallelograms:

$3^2:4^2=9:16$

Answer

9:16

Exercise #3

Is rectangle ABCD similar to rectangle EFGH?

Video Solution

Step-by-Step Solution

We first need to verify the ratio of similarity.

We examine if:

$\frac{AB}{EF}=\frac{AC}{EG}$

To do this, we substitute our values in:

$\frac{7}{10}=\frac{3}{6}$

$\frac{7}{10}\ne\frac{1}{2}$

The ratio is not equal, therefore the rectangles are not similar.

Answer

Exercise #4

In front of you are two hexagons with a similarity ratio. Which angles are corresponding?

Video Solution

Answer

Angle C = Angle O

Exercise #5

Which shapes are similar?

Video Solution

Answer

The rectangles are similar.

Do you know what the answer is?

Question 1

Which shapes are similar?

Question 2

Which figure shows a pair of similar polygons?

Question 3

Which statement is true?

Start practice