Similar Triangles

We will illustrate the issue with an example.

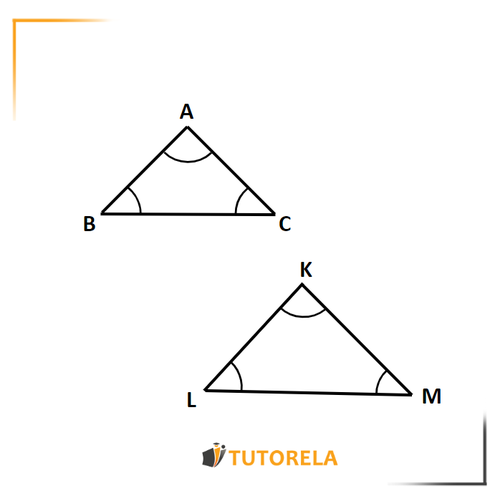
The drawing before us shows two similar triangles,$\triangle ABC$ and $\triangle KLM$.

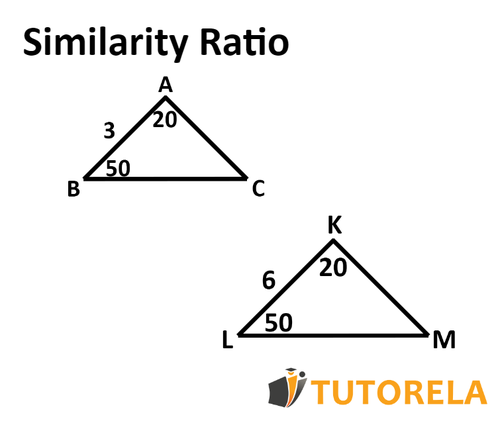
The similarity ratio of the triangles is $2$. This means that each side in the larger triangle $\triangle ABC$ is twice as large as the corresponding side in the smaller triangle $\triangle KLM$.

In addition, the angles at the corresponding places in the two triangles are equal to each other.

As illustrated in the drawing, the following is true:

The angle $\sphericalangle A$ is equal to the angle $\sphericalangle K$
The angle $\sphericalangle B$ is equal to the angle $\sphericalangle L$
The angle $\sphericalangle C$ is equal to the angle $\sphericalangle M$

If you are interested in this article you may also be interested in the following articles

• Similarity of Triangles and Polygons
• Similarity Ratio
• Criterion of similarity between two triangles
• Similarity of geometric figures

In Tutorela you will find a great variety of mathematics articles.

Task

If we are talking about similar triangles then:

Choose the correct answer.

Solution

In similar triangles, the ratio of the lengths of the sides of two similar triangles is equal to the ratio of their perimeters.

Answer

The ratio of the lengths of the sides of two triangles is equal to the ratio of their perimeters.

The ratio of the area of similar triangles is $\frac{9}{100}$.

If we are given that the perimeter of the large triangle is $129\operatorname{cm}$, what is the perimeter of the small triangle?

Solution

$\frac{S\triangle}{S\triangle}=\frac{9}{100}$

The ratio of the sides is

$\frac{3}{10}$

$\frac{P\triangle}{P\triangle}=\frac{P\triangle}{129}=\frac{3}{10}$

The perimeter of the small triangle is $38.7$

Answer

$38.7$

Task

Given two similar triangles. The area of the small triangle is $12.5$, what is the length of the side?

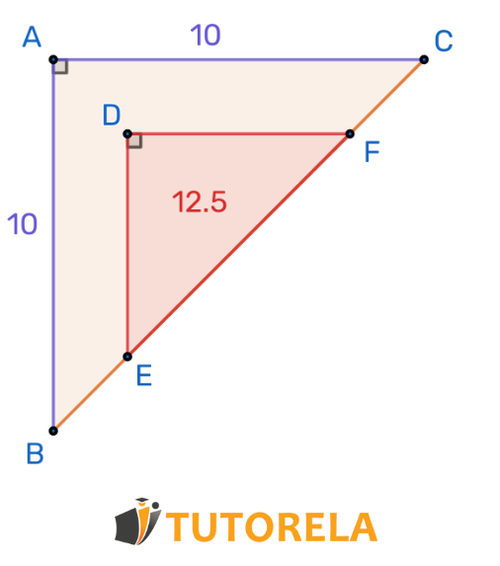
Area of the large triangle

$\frac{10\times10}{2}=50$

The area of the small triangle is $12.5$

$\frac{50}{12.5}=4$

$\sqrt{4}=2$

$\frac{10}{x}=2$

$x=5$

Answer

$5$

Question

What is the area of the blue triangle if it is given that the two triangles are similar and the area of the green triangle is $64$.

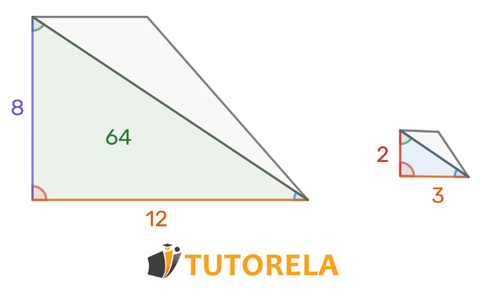
Solution

From the similarity it follows that $\frac{12}{3}=4$

$\frac{64}{S}=16$

$\frac{64}{16}=S$

$S=4$

Answer

$4$

Task

The ratio of similarity between two similar triangles is $7$, then the ratio of the areas is $_{——}$

Solution

In general, this question is based on the simple "rule": the ratio of the area is equal to the square of the similarity ratio

Then, if the ratio of similarity is $7$,

the ratio of the areas is $7^2$

which is $49$

Answer

$49$

What are two similar triangles?

We can say that two triangles are similar when they have the same shape even if they have different sizes, for that they must meet some of the similarity criteria.

What are the three similarity criteria?

To know that two triangles are similar they must meet some of the three similarity criteria:

• Side-Side-Side (SSS): If the ratio of their three pairs of corresponding sides is the same then two triangles are similar.
• Side-Angle-Side (SAS): Two triangles are similar if the ratio of two pairs of corresponding sides is the same and the angle between these two pairs is the same, then they are similar triangles.
• Angle-Angle (AA): For two triangles to be similar by this criterion, two of their respective angles must measure the same and therefore the third angle must also have the same measure as the angle corresponding to that angle. That is, their three corresponding angles measure the same.

What is the ratio of similarity of two triangles?

It is the ratio between the corresponding sides of those triangles.

How to find the similarity ratio of two triangles?

The similarity ratio is obtained by dividing the corresponding sides of two similar figures, in this case of two triangles.

Let's see an example:

Task

Given the following similar triangles $\triangle ABC\sim\triangle DEF$

Calculate the similarity ratio

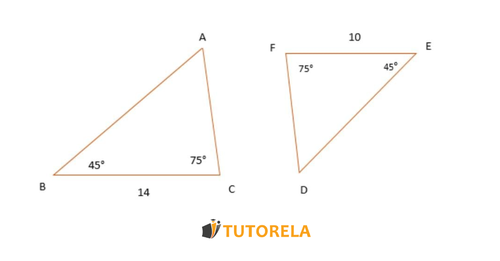
Given that $\triangle ABC\sim\triangle DEF$ by the similarity criterion AA.

Then we must locate which are the corresponding sides, and from here we deduce that

$\sphericalangle A=\sphericalangle D$

$\sphericalangle B=\sphericalangle E$

Then the corresponding sides are $AB$ and $DE$

Now to calculate the similarity ratio we do the quotient of these two sides.

$\frac{AB}{DE}=\frac{15}{10}=\frac{3}{2}=1.5$

Answer

$1.5$

What is the difference between two similar triangles and congruent triangles?

The difference is that when two triangles are similar they have the same shape but their corresponding sides do not have to have equal sides, while when two triangles are congruent they have the same shape AND their corresponding sides are equal.

Exercise of similarity of triangles

Task

Demonstrate that the following triangles are similar

From the above we can observe that they have two pairs of equal angles

$\sphericalangle B= 45°= \sphericalangle E$

$\sphericalangle C= 75°= \sphericalangle F$

Then we say that the triangles are similar by the similarity criterion AA. They have the same shape but in different position.

Answer

$\triangle ABC\sim\triangle DEF$