Quadratice Equations and Systems of Quadraric Equations

Quadratic Equations System

To find the solution of the system of quadratic equations (points of intersection of the functions) we will act as follows:

We will verify that the unknown $Y$ is written the same way in both equations
We will compare the equations
Let's find the $X$
Gradually place an $X$ in one of the equations to solve for its $Y$ .
Let's neatly record the answers we find.

Detailed explanation

Start practice

Test yourself on equations and systems of quadratic equations!

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

Practice more now

Quadratic Equations System

We already learned that we should not fear the word "system". Don't worry, even when it comes to a system of quadratic equations, which are not linear, the solution is simple and straightforward.
Systems of quadratic or second-degree equations are quadratic equations written together, one next to the other or one below the other with a curly bracket, similar to what we already studied for systems of linear equations.
Generally, $X$ and $Y$ would not have been given to us, therefore, they are our unknowns.
When the problem states "given the system of equations" you should know that the result has to be $X$ and $Y$ that meet the conditions of said system.
The system can have one solution, two solutions, or even none.
The meaning of the solution of the system of equations is demonstrated by the points of intersection of the functions.
At those very points, the functions meet, they intersect.
These specific points exist in both the first equation and the second.

Algebraic Solution

To solve a system of quadratic equations, we will use the comparison method between quadratic equations
When we have a system of quadratic equations and the $Y$ isolated in this way (with the same coefficient in both equations):

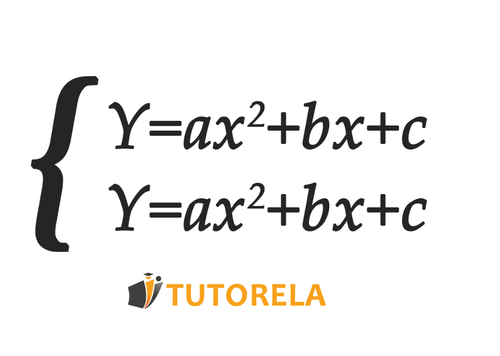
We will proceed in the following order:
We will verify that the unknown $Y$ is written the same way in both equations
We will compare the equations

We will find the $X$
We will gradually place an $X$ in one of the equations to solve for its $Y$ .
We will neatly record the answers found.

Note
The coefficients of the unknown and the various parameters do not necessarily have to be the same, except for the unknown $Y$ . When comparing equations, first verify that the unknown $Y$ is written in the same way in both equations
Let's see an example of solving a system of equations using the comparison method between quadratic equations:
Given the following system of equations:

2 - the following system of equations Y=X²+2X-8 and Y=-X²-X+12

We will proceed step by step:

We will verify that the unknown $Y$ is written the same way in both equations
The unknown $Y$ indeed appears the same way in both equations, its coefficient is $1$ .
We will compare the equations
$x^2+2x-8=-x^2-x+12$
We will find the $X$
We will solve this equation as an equation with $1$
unknown:
$x^2+2x-8=-x^2-x+12$

We will transpose sides:
$2x^2+3x-20=0$

We will solve the quadratic equation (with the quadratic formula) and obtain:
$X=2.5 ,-4$
We will gradually place an $X$ in one of the equations (the original) to solve for its $Y$
Let's start with $X=2.5$
We will place it in the selected equation within the system of equations (it doesn't matter which one, it's advisable to choose the one that seems easier):

$Y=-x^2-x+12$
We will place $X=2.5$
We will obtain:

$Y=-(2.5)^2-2.5+12$
$y= -6.25-2.5+12$
$y=3.25$

Let's write down this result: $( 3.25 , 2.5)$

Now let's move on to the second $X$ .
$X=-4$

We will place it in the selected equation within the system of equations (it doesn't matter which one)
$Y=-x^2-x+12$
We will place $X=-4$ Remember to use parentheses to avoid confusion with the signs for addition and subtraction

We will obtain:
$Y=-(-4)^2-(-4)+12$
$Y=-16+4+12$
$y=0$
Let's write down this solution:

$( 0 , -4)$

5. Let's neatly record the answers we found.

$( 0 , -4) , ( 3.25 , 2.5)$
Now let's move on to the graphical method, so we can better understand the meaning of the solution to the system of equations.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Observe the rectangle below.

$$ x>0 $$

If the area of the rectangle is:

$$ x^2-13 $$ .

Calculate x.

Question 2

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0$

Solve the above equations by completing the square/ factoring:

$(a+by)^2(a-by)=\text{?}$

Question 3

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

Graphical Solution

The graphical solution of the system of quadratic equations are the points of intersection of the parabolas.
Therefore, when the parabolas are graphically represented, the solution of the system of equations will be their points of intersection.
If they do not intersect, it means that the system of equations has no solution.

For example

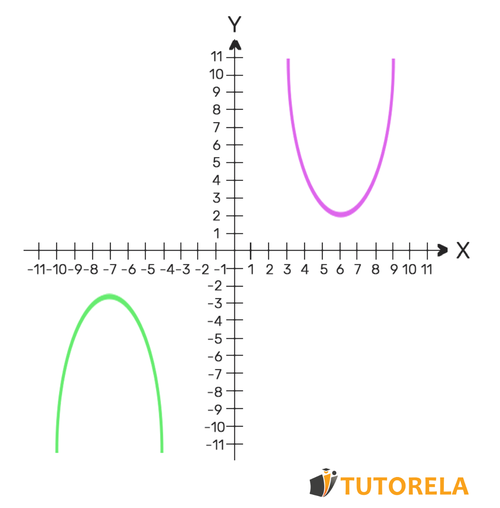
If cut once, the system of equations will have one solution - the intersection point of the parabolas.

For example

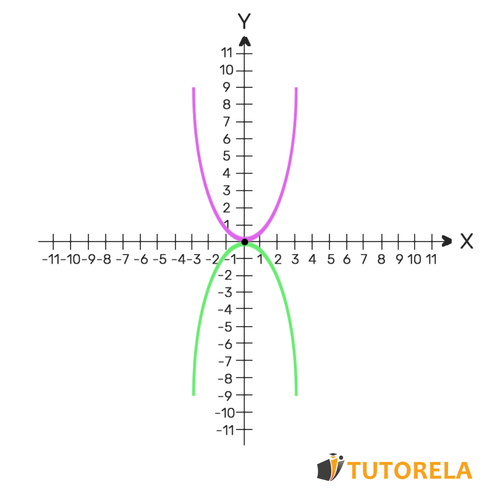
4 - the intersection point of the parabolas

If they intersect twice, the system of equations will have two solutions - the intersection points of the parabolas.

For example

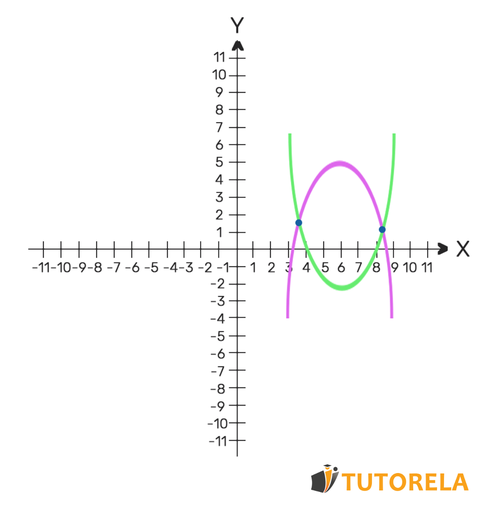
5 - System of equations with two solutions

Now, let's move on to the system of combined equations – that is, one linear and the other quadratic.

Solution of a system of equations when one of them is linear and the other quadratic

In case the system of equations is composed of a quadratic equation and a linear equation, in the following way:
$Y=ax^2+bx+c$
$y=mx+n$

We will use the substitution method

Substitution method: It allows us to substitute the value of the variable y in an equation, thereby obtaining an equation with one variable.
Again, let's remember to neatly place the variable in parentheses to avoid confusion.

Note: Equations can be arranged in a different way, for example, the linear equation does not have to be represented in the same way seen previously and could have a coefficient that is not $Y$ .

Let's see it in an example:

Example of using the substitution method

Given the system of equations (combined):
$Y=2x^2-5x+1$
$3x+2y=17$

We will notice that the equations are written differently from each other (in one the $Y$ is isolated and in the other it is not) and there is no problem with this.
To use the substitution method, we generally need to completely isolate one of the variables in the equations.
Now, we can place the value of $Y$ (the first quadratic equation) into the linear equation and obtain a linear equation with one unknown.
Remember to use parentheses to avoid confusion.
Let's see:

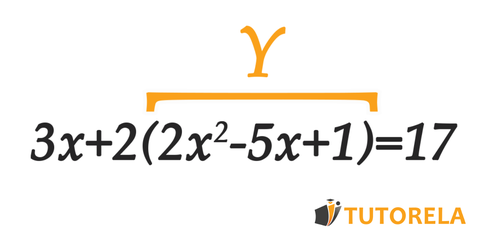
6 - Example of using the substitution method

Let's remove the parentheses and we will get:
$3x+4x^2-10x+2=17$
Let's combine like terms and we will get:
$-7x+4x^2+2=17$
Let's arrange the equation, transpose terms and we will get:
$4x^2-7x-15=0$
Let's solve with the quadratic formula and we will get:
$x=3 ,-\frac{5}{4}$
Now, let's remember to place the found $X$ values to find the $Y$ values and thus be able to reach a complete result.
We will start with $x=3$ and place it in one of the original equations (the one that seems simpler - which is generally the linear one)
We will get:
$3 \times 3+2y=17$
$9+2y=17$
$2y=8$
$y=4$
Let's write this solution: $(4 , 3)$
Now let's place the second $X$ we found, in one of the original equations and we will get: $x=-\frac{5}{4}$

$3 \times (--\frac{5}{4})+2y=17$

$-\frac{15}{4}+2y=17$
$2y=20.75$
$y=10.375$
Let's write this solution: $(10.375 , -\frac{5}{4})$

Let's neatly note down the solutions found $(4 , 3) , (10.375 , -\frac{5}{4})$
These are the points of intersection of the line with the parabola.

Do you know what the answer is?

Question 1

Observe the rectangle below.

$$ x>0 $$

If the area of the rectangle is:

$$ x^2-13 $$ .

Calculate x.

Question 2

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0$

Solve the above equations by completing the square/ factoring:

$(a+by)^2(a-by)=\text{?}$

Question 3

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

Intersection between two parabolas

Parabolas located on the same Cartesian plane can intersect more than once.
To find the intersection points between the parabolas, we should compare their equations, as we have learned, when $Y$ appears in the same way in both equations (with the same coefficient).
By comparing the equations, we will arrive at an equation with one unknown $X$ .
We will solve for the value of $X$ and alternately place in each of the equations the value of $X$ to discover $Y$ .
If we arrive at one solution, it means that the parabolas intersect only once.
If we arrive at two solutions, it means that the parabolas intersect twice.
If we find that there is no solution, it means that the parabolas do not intersect at all.

Useful Information
In some cases, as in the example, the parabolas may intersect when $X=5$
And the question will be what are the intersection points of the parabolas.
To find the intersection points, we simply place $X=5$ in one of the given parabola equations and thus discover the point.

Word Problems

We must convert verbal math problems into quadratic equations to solve them
Just as we have already done, equations are constructed based on the text given in the problem.
How will we do it?
The key to solving problems of this type is to describe the unknowns through a single unknown $X$ .
This way instead of arriving at two equations with two unknowns we will arrive at one quadratic equation.
Another very important issue is to read and understand exactly what the problem is telling us. This way we can construct the equation correctly.
Let's see an example:
Find two numbers whose sum equals $11$ and the sum of these squared equals $61$
Solution:
First, let's define the variables with one unknown
First number: $X$
Second number: $11-X$
How have we defined the second number?
We know that the sum of the two numbers we are looking for is $11$
Think about this: let's say the second number was $Y$ ,
we would write
$y+x=11$
and isolate the $Y$
We would get $Y=11-X$
Magnificent. Now let's move on to the second part of the problem: the sum of the numbers squared equals $61$ That is, if we square each of the numbers and then add them we will get $61$
Let's translate it into an equation:
$X^2+(11-x)^2=61$

Great! Now let's remove the parentheses using the distributive property of multiplication and we will arrive at a sorted quadratic equation:

$x^2+121-22x+x^2=61$

Let's combine terms and we will get:
$2x^2-22x+60=0$

Great! We can solve this quadratic equation easily with the quadratic formula. Let's solve and we will get to:

$X=6.5$

Pay attention! These are not the two numbers we are looking for! These are possible solutions for the first number.
Now we must find what the second number would be in each of these possibilities.
Let's begin:
When the first number is $5$ ,
the second is $11-X$ and therefore, $6$ .
When the first number is $6$ ,
the second is $11-X$ and therefore $5$ .

Check your understanding

Question 1

Observe the rectangle below.

$$ x>0 $$

If the area of the rectangle is:

$$ x^2-13 $$ .

Calculate x.

Question 2

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0$

Solve the above equations by completing the square/ factoring:

$(a+by)^2(a-by)=\text{?}$

Question 3

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

Quadratic Inequality

The quadratic inequality describes in which interval the function is positive and in which it is negative.
You have already studied all the steps to solve an inequality of this type.
Before we begin to learn how to solve the quadratic inequality, it is advisable to remember two important things:

Set of positivity and negativity of the function:
Set of positivity - represents the $X$ in which the graph of the parabola is above the $X$ axis, with a positive $Y$ value.
Set of negativity - represents the $X$ in which the graph of the parabola is below the $X$ axis, with a negative $Y$ value.
Dividing by a negative term - reverses the sign of the inequality.

Excellent, now we can begin.
When we have a quadratic inequality, we will act following these steps:

Transposition of terms and isolation of the quadratic equation until one side equals $0$ . Remember that when we divide by a negative term, the inequality is reversed.
Drawing a parabola scheme - placing points of intersection with the $X$ axis and identifying the maximum and minimum of the parabola.
Calculation of the corresponding interval according to the exercise and the scheme.
Interval of positivity: $0<$ quadratic equation
Interval of positivity: $0>$ quadratic equation

Let's look at an example

Solve the following inequality:
$x^2+x-30<0$

Solution:
Let's proceed step by step:

Let's make sure that on one side we have $0$ In the case of the example, the equation is already in this form.
Let's draw a diagram.

Let's find the points of intersection with the $X$ axis
$x^2+x-30=0$
According to the quadratic formula, we will obtain:
$X=5,-6$

We will identify, according to the coefficient of $x^2$ , that the parabola opens upwards.

Let's draw a diagram

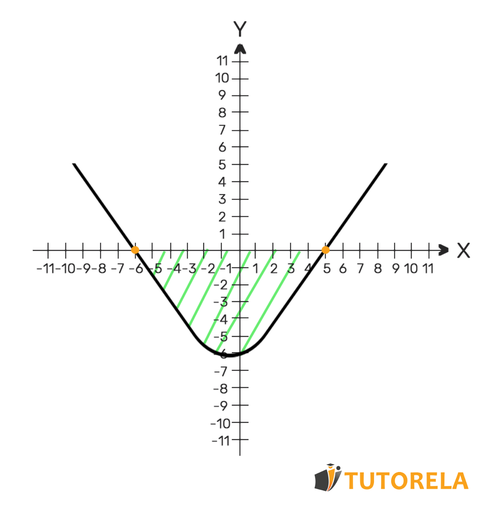
7 - We will identify based on the coefficient of x^2 that the parabola is the minimum

Let's calculate the corresponding interval according to the exercise and the scheme.
$x^2+x-30<0$

Since the exercise asks when the quadratic equation is less than $0$ , they are asking about the interval of negativity, therefore, by observing the scheme we can determine that the quadratic equation is less than $0$ when :
$-6<x<5$
This is the solution to the inequality.

Examples and exercises with solutions of systems of quadratic equations

Exercise #1

Consider the following relationships between the variables x and y:

$x^2+4=-6y$

$y^2+9=-4x$

Which answer is correct?

Video Solution

Step-by-Step Solution

To determine the correct relationship between $x$ and $y$ , let's transform each equation:

Step 1: Transform the First Equation

The first equation is $x^2 + 4 = -6y$ . Rearranging gives us:

$x^2 = -6y - 4$

Now, aim to complete the square for expressions involving $x$ and $y$ .

Step 2: Transform the Second Equation

The second equation is $y^2 + 9 = -4x$ . Rearranging gives us:

$y^2 = -4x - 9$

Step 3: Complete the Square

Let's complete the square for the terms $x^2$ and $y^2$ .

For $x^2 = -6y - 4$ :

$x^2 + 4x + 4 = -6y$

Thus, it becomes:

$(x + 2)^2 = -6y$

For $y^2 = -4x - 9$ :

$y^2 + 6y + 9 = -4x$

Thus, it becomes:

$(y + 3)^2 = -4x$

Step 4: Combine and Analyze

Substitute back to express a sum of squares:

Adding these completes the square:

$(x + 2)^2 + (y + 3)^2 = 0$

This result shows that both squares, squared terms are zero-sum, revealing the conditions under which equations balance.

Thus, the correct choice according to the transformations conducted is:

$(x+2)^2 + (y+3)^2 = 0$

Therefore, the solution to the problem is $(x+2)^2 + (y+3)^2 = 0$ .

Answer

_{^{$(x+2)^2+(y+3)^2=0$}}

Exercise #2

Observe the rectangle below.

$x>0$

If the area of the rectangle is:

$x^2-13$ .

Calculate x.

Video Solution

Step-by-Step Solution

First, recall the formula for calculating the area of a rectangle:

The area of a rectangle (which has two pairs of equal opposite sides and all angles are $90\degree$ ) with sides of length $a,\hspace{4pt} b$ units, is given by the formula:

$\boxed{ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=a\cdot b }$ (square units)

After recalling the formula for the area of a rectangle, let's proceed to solve the problem:

Begin by denoting the area of the given rectangle as: $S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}$ and proceed to write (in mathematical notation) the given information:

$S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2-13$

Continue to calculate the area of the rectangle given in the problem:

Using the rectangle area formula mentioned earlier:

$S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=a\cdot b\\ \downarrow\\ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=(x-4)(x+1)$

Continue to simplify the expression that we obtained for the rectangle's area, using the distributive property:

$(c+d)(h+g)=ch+cg+dh+dg$

We are able to obtain the area of the rectangle by

using the distributive property as shown below:

$S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=(x-4)(x+1) \\ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2+x-4x-4\\ \boxed{ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2-3x-4}$

Recall the given information:

$S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2-13$

Therefore, we can conclude that:

$x^2-3x-4=x^2-13 \\ \downarrow\\ -3x=4-13\\ -3x=-9\hspace{6pt}\text{/}(-3)\\ \boxed{x=3}$

We solved the resulting equation simply by combining like terms, isolating the expression with the unknown on one side and dividing both sides by the unknown's coefficient in the final step,

Note that this result satisfies the domain of definition for x, which was given as:

$-1\text{<}x\text{<}4$ and therefore it is the correct result

The correct answer is answer C.

Answer

$x=3$

Exercise #3

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases}$

Solve the above equations by completing the square/ factoring:

$(a+by)^2(a-by)=\text{?}$

Step-by-Step Solution

In this problem we are required to calculate the value of the expression:

$(a+by)^2(a-by)=\text{?}$

This is without solving the system of equations,

Let's examine the given system:

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases}$

In this system there are two equations with two unknowns and two parameters, one of the equations is of a higher degree, and the second is of first degree,

From which we need to calculate the value of the requested expression, without solving the system,

Let's try to find hints in the question and find another "trick", for this we can first notice that the expression:

$ax+by$

Which appears inside the multiplication on the right side in the first equation, can also be found in the second equation, by opening parentheses and moving terms:

$( a(x+1)=-by\\ \downarrow\\ ax+a=-by\\ \boxed{ax+by=-a}$

In other words, we can substitute the value of this expression completely in the first equation, let's do this (for convenience in calculation we'll show the complete system of equations):

$\begin{cases} a^2x^3+2abx^2y=-2a\textcolor{red}{(ax+by)}\\ a(x+1)=-by\rightarrow \boxed{\textcolor{red}{ax+by=-a}} \end{cases} \\ \downarrow\\ a^2x^3+2abx^2y=-2a\textcolor{red}{(-a)}\\ \boxed{a^2x^3+2abx^2y=2a^2}$

We have therefore received a simpler equation, but still of a higher degree with two unknowns, let's try to reduce the degree of the expression on the left side,

Note that in this expression we can factor out a common term:

$a^2x^3+2abx^2y=2a^2\\ \downarrow\\ x(a^2x^2+2abxy)=2a^2$

Now let's look at the expression in parentheses, and think again about the second equation we got in the system of equations:

$\begin{cases} x(\textcolor{blue}{a^2x^2+2abxy})=2a^2\\ ax+by=-a \end{cases} \\$

We can see that, by completing the square in the expression, we can use the second equation again, this is done by presenting the expression in parentheses as a binomial squared plus a correction term, remember that for this we need to identify the missing term in the expression so we can complete the square, and then add and subtract it from the expression:

$x(a^2x^2+2abxy)=2a^2\\ \downarrow\\ x\big((ax)^2+2axby\big)=2a^2\\\\ x\big((ax)^2+2axby+\underline{\underline{(by)^2-(by)^2}}\big)=2a^2\\ x\big((\textcolor{red}{ax})^2+2\textcolor{red}{ax}\textcolor{green}{by}+(\textcolor{green}{by})^2-b^2y^2\big)=2a^2\\ \downarrow\\ x\big((\textcolor{red}{ax}+\textcolor{green}{by})^2-b^2y^2)=2a^2$

Let's now show the system of equations we got after the last step, then we'll substitute the value of the expression from the second equation into the first equation (bottom line) and simplify:

$\begin{cases} x(a^2x^2+2abxy)=2a^2\\ ax+by=-a \end{cases} \\ \downarrow\\ \begin{cases} x\big((\underline{ax+by})^2-b^2y^2\big)=2a^2\\ ax+by=-a \end{cases} \\ \downarrow\\ x\big((\underline{-a})^2-b^2y^2\big)=2a^2\\ x(a^2-b^2y^2)=2a^2$

Now we can examine our goal - calculating the value of the expression:

$(a+by)^2(a-by)=\text{?}$

We can see that we are already very close to getting the value of this expression from the equivalent system of equations we received (we'll also note the second equation):

$\begin{cases} x(a^2-b^2y^2)=2a^2\\ ax+by=-a \end{cases} \\$

We can now use factoring using the difference of squares formula, and factor the expression in parentheses, we can also now isolate x from the second equation, let's do this in parallel:

$\begin{cases} x(a^2-b^2y^2)=2a^2\\ ax+by=-a \end{cases} \\ \downarrow\\ \begin{cases} x(a^2-(by)^2)=2a^2\\ ax=-(a+by)\hspace{6pt}\text{/}:a \end{cases} \\ \downarrow\\ \begin{cases} x(a+by)(a-by)=2a^2\\ x=-\frac{a+by}{a} \end{cases} \\$

Now let's substitute the isolated unknown in the first equation, identify the requested expression, and calculate its value by isolating it:

$\begin{cases} \textcolor{blue}{x}(a+by)(a-by)=2a^2\\ \textcolor{blue}{x=-\frac{a+by}{a}} \end{cases} \\ \downarrow\\ -\frac{a+by}{a}\cdot(a+by)(a-by)=2a^2 \\ -\frac{(a+by)(a+by)(a-by)}{a}=2a^2\hspace{6pt}\text{/}\cdot (-a)\\ \boxed{(a+by)^2(a-by)=-2a^3}$

Therefore the correct answer is answer D

Answer

$-2a^3$

Do you think you will be able to solve it?

Question 1

Observe the rectangle below.

$$ x>0 $$

If the area of the rectangle is:

$$ x^2-13 $$ .

Calculate x.

Question 2

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0$

Solve the above equations by completing the square/ factoring:

$(a+by)^2(a-by)=\text{?}$

Question 3

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

Start practice