Quadratic Equations System - Algebraic and Graphical Solution

Quadratic Equations System

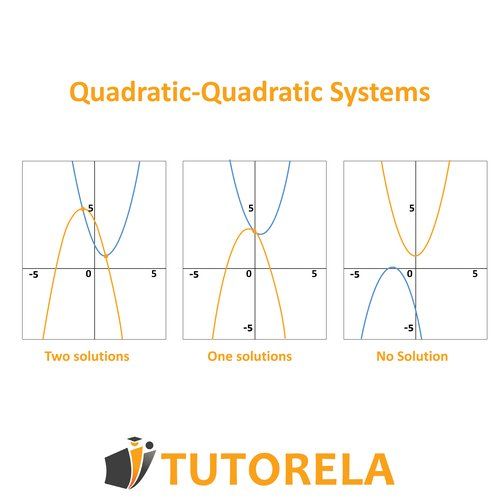
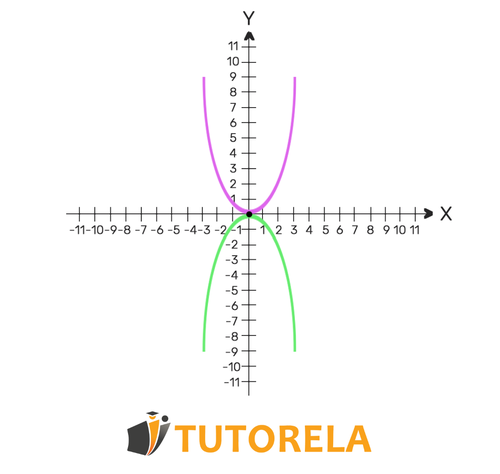
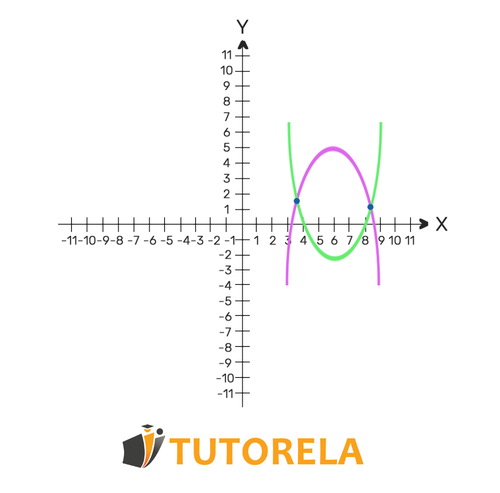
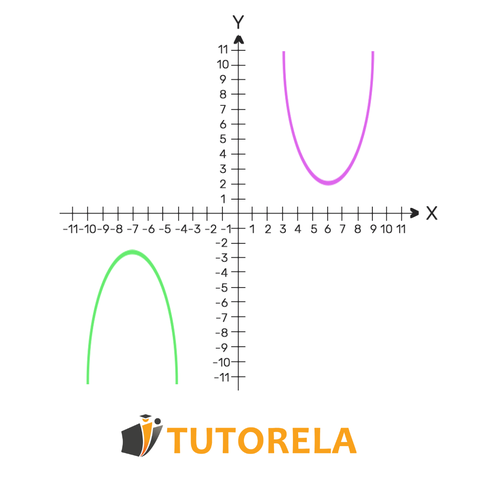
In the system of quadratic equations, we must find the $X$ and $Y$ that satisfy the first equation as well as the second. The system can have one solution, two solutions, or even none. The concept of the solution of the system of equations highlights the points of intersection of the function. At the same points we find - the functions intersect. If one solution is found - the functions intersect once. If two solutions are found - the functions intersect twice. If no solution is found - the functions never intersect.

Detailed explanation

Start practice

Test yourself on systems of quadratic equations!

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

Practice more now

Algebraic solution

Method: Comparison between quadratic equations

When we have a system of quadratic equations and the $Y$ is isolated in this way (with the same coefficient in both equations):
$Y=ax^2+bx+c$
$Y=ax^2+bx+c$

We will proceed in the following order:

We will verify that the variable $Y$ is written in the same way in both equations
We will compare the equations
We will solve for the $X$ s
We will gradually substitute $X$ s into one of the equations to solve for its $Y$
We will neatly record the solutions we have found.

Attention - The other parameters do not necessarily have to be the same. Only the $Y$ needs to be isolated in the same way in order to equate the equations.

Graphical solution

The solution of the system of quadratic equations represents the points of intersection of the parabolas. Therefore, we will be able to see the solution of the system of equations graphically as the points of intersection of the parabolas.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Look at the rectangle in the figure.

$$ x>0 $$

The area of the rectangle is:

$$ x^2-13 $$ .

Calculate x.

Question 2

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0$

Solve the above equations by completing the square/ factoring:

Make sure to explain the steps , and show your work: , including all calculations:

$(a+by)^2(a-by)=\text{?}$

Question 3

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

If a solution is found - the functions intersect only once

If two solutions are found - the functions intersect twice

Do you know what the answer is?

Question 1

Look at the rectangle in the figure.

$$ x>0 $$

The area of the rectangle is:

$$ x^2-13 $$ .

Calculate x.

Question 2

$\begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0$

Solve the above equations by completing the square/ factoring:

Make sure to explain the steps , and show your work: , including all calculations:

$(a+by)^2(a-by)=\text{?}$

Question 3

Consider the following relationships between the variables x and y:

$$ x^2+4=-6y $$

$$ y^2+9=-4x $$

Which answer is correct?

If no solution is found - the functions never intersect

Let's look at an example

$y=5x^2-2x+6$
$y=-5x^2-2x+6$

Let's verify that the $Y$ is really isolated in the same way.
Let's compare the equations:
$5x^2-2x+6=-5x^2-2x+6$
Let's solve for $X$ s
$5x^2-2x+6=-5x^2-2x+6$
Let's transpose terms and we will get:
$10x^2=0$
$x^2=0$
$x=0$
Let's find the $Y$ by substituting the $X$ we found into one of the equations:
$y=5x^2-2x+6$
$y=5*0^2-2*0+6$
$y=6$
Let's note the solution we found: $(6, 0)$
at this point the functions intersect and that is the solution to the system of equations.