Opposite numbers | Tutorela

In the previous articles we studied about the number line and integers. In this article we will explain what opposite numbers are, and how to identify them.

What are opposite numbers, and how to identify them?

Opposite numbers are numbers that when added together result in the number $0$ .

The opposite of a number has the same absolute value, but with opposite sign.

Examples:

$+3$ and $-3$ are opposite numbers.
$+9.4$ and $-9.4$ are opposite numbers.
$+\frac{1}{4}$ and $-\frac{1}{4}$ are opposite numbers (fractions).

B - What are opposite numbers, and how to identify them

Detailed explanation

Start practice

Test yourself on basic definitions!

What is the inverse number of $$ 0.7 $$

Practice more now

As we have already studied in previous articles, in positive numbers, the plus sign can be omitted.
So it is that:

$8$ and $-8$ are opposite numbers.
$+100$ and $-100$ are opposite numbers.

As we have already said, when we add two opposite numbers, the result is $0$ .
Examples:

$(-5)+(+5)=0$
$(+54)+(-54)=0$
$23.5+(-23.5)=0$

Also when we add $0 + 0$ the result is zero. Therefore, the number opposite zero is zero itself. This is a special case.

Do the following exercises, applying what we have studied in this article:

Of the following numbers, which pairs are opposite numbers?

$+7, -4$
$9.4, -9.4$
$+4.35, -4.35$
$80, +80$
$+313, -313$
$0, 0$
$-45, +54$

2. Create $8$ addition operations, in which the result of each one of these will give us $0$ .

3. Fill in the blanks, to get the number opposite the number shown.

$4$ $-3+$ __
$-8$ $20+$ __
$-33$ __ $+(+10)$
$60$ $-64+$ __
$0$ $18+$ __

4. What is the opposite of the following numbers?

$0.7$
$5$
$-0.25$
$87$
$-7$
$-{8\over7}$

5. Based on what you have learned about the topic absolute value Determine if the following pairs of numbers are opposites:

$-|-81| , |92|$
$|-3| , |3|$
$|56| , |-5.6|$
$-|-801| , |+801|$
$∣-\frac{1}{3}∣,∣\frac{3}{1}∣$
$∣−8∣,∣\frac{64}{8}∣$

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

What is the additive inverse number of $$ 87 $$

Question 2

What is the inverse number of $$ 5 $$

Question 3

What is the inverse number of $$ -7 $$

If you are interested in this article you may also be interested in the following articles

Positive and negative numbers and zero

The real line

Absolute value

Elimination of parentheses in real numbers

Addition and subtraction of real numbers

Multiplication and division of real numbers

On the Tutorela blog you will find a variety of articles about mathematics.

Review questions

What are the opposite or symmetrical numbers?

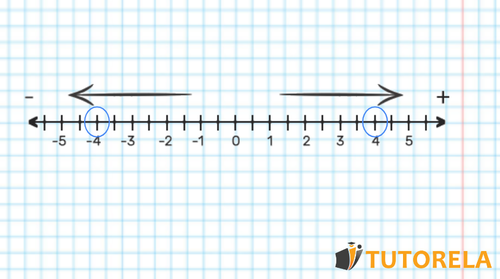
The opposite numbers or also called symmetric numbers are those that have the same number, but with opposite sign, we can also define them as those numbers that are at the same distance from zero on the number line. For example, in the following line we have $-4$ and $4$ these two numbers are symmetrical, since they have different signs and are at the same distance from zero.

1 - Different sign and they are at the same distance from zero

Do you know what the answer is?

Question 1

$$ (+43)-(+15)= $$

Question 2

$$ (+71)+(-18)= $$

Question 3

What is the inverse number of $$ -0.25 $$

What do the opposite numbers mean?

They mean that they are at the same distance from zero, opposite numbers mean that they have the same quantity but with different signs, for example: $6$ and $-6$ or $-14$ and $14$ .

How to make the opposite numbers?

In order to find the opposite or symmetric numbers we just write the same number but with the opposite sign, for example we are going to write the opposites of the following numbers:

$-9$ we write again the same number but in this case as it is negative then its symmetric will be positive. $9$
$3.5$ its symmetric number will be the same number but with opposite sign, that is, $-3.5$
$\frac{3}{5}$ we write the same number but with opposite sign $-\frac{3}{5}$ .

Ejemplos y ejercicios con soluciones de números opuestos

Exercise #1

What is the inverse number of $-7$

Video Solution

Step-by-Step Solution

To solve the problem of finding the opposite number of $-7$ , we will use the concept of opposite numbers:

Step 1: Identify the given number, which is $-7$ .
Step 2: Determine the opposite number by changing the sign. The opposite of $-7$ is calculated as follows:

The opposite of a negative number is its positive counterpart. So, the opposite of $-7$ is $7$ .

Therefore, the answer is $7$ .

Answer

$7$

Exercise #2

What is the inverse number of $5$

Video Solution

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Identify the given number.
Step 2: Find its opposite by changing the sign.

Now, let's work through each step:
Step 1: The problem gives us the number $5$ .
Step 2: The opposite of a positive number is the same number with a negative sign.
Thus, the opposite of $5$ is $-5$ .

Therefore, the opposite number of $5$ is $-5$ .

Answer

$-5$

Exercise #3

What is the additive inverse number of $87$

Video Solution

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Identify the given number
Step 2: Apply the definition of an opposite number
Step 3: Conclude with the opposite number

Now, let's work through each step with detailed explanations:
Step 1: We are given the number $87$ . This is a positive integer.
Step 2: The definition of an opposite number states that the opposite of any number $x$ is $-x$ . Here, $x = 87$ .
Step 3: Using the definition, the opposite number of $87$ is calculated as $-87$ .

Therefore, the solution to the problem is $-87$ .

Answer

$-87$

Exercise #4

What is the inverse number of $0.7$

Video Solution

Step-by-Step Solution

To determine the opposite number of $0.7$ , we will simply change its sign, following these steps:

Step 1: Identify the given number, which is $0.7$ .
Step 2: Change the sign of $0.7$ to find its opposite. Since $0.7$ is positive, its opposite will be negative.

By changing the sign of $0.7$ , we get $-0.7$ . Therefore, the opposite number of $0.7$ is $-0.7$ .

In conclusion, the solution to the problem is $-0.7$ .

Answer

$-0.7$

Exercise #5

What is the inverse number of $-\frac{8}{7}$

Video Solution

Step-by-Step Solution

To determine the opposite number of $-\frac{8}{7}$ , we need to understand what the opposite of a number means in mathematics.

The opposite of a number is simply a number with the same magnitude but the opposite sign. For any real number $a$ , its opposite is $-a$ . When $a$ is already negative, its opposite is positive.

Given the number $-\frac{8}{7}$ , we will apply the following steps:

Identify the sign and magnitude: The given number is $-\frac{8}{7}$ , a negative fraction.
Apply sign change: The opposite is simply the positive version of $-\frac{8}{7}$ , which is $\frac{8}{7}$ .

Thus, the opposite of $-\frac{8}{7}$ is $\frac{8}{7}$ .

Therefore, the correct answer is $\frac{8}{7}$ .

Answer

$\frac{8}{7}$

Check your understanding

Question 1

What is the inverse number of $-\frac{8}{7}$

Question 2

$(+0.5)+(+\frac{1}{2})=$

Question 3

$(-2^2)-(-3\frac{3}{4})=$

Start practice