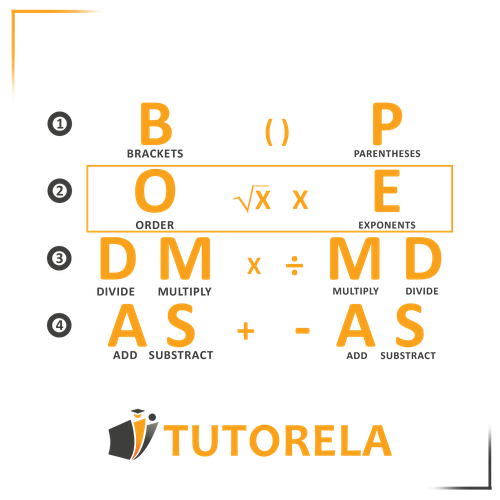
The second step in the order of operations is - exponents and roots!
Order of Operations with Exponents and Roots Practice Problems
Master PEMDAS with exponents and square roots! Practice order of operations problems step-by-step with detailed solutions and instant feedback.
📚Master Exponents and Roots in Order of Operations
- Solve expressions with exponents following proper PEMDAS order
- Calculate square roots and higher roots within complex expressions
- Handle parentheses containing exponents and roots correctly
- Apply exponent rules including zero power and negative bases
- Work through multi-step problems with mixed operations systematically
- Identify and avoid common mistakes in order of operations
Understanding Powers and Roots
Complete explanation with examples
Order of Operations - Exponents and Roots
Immediately after dealing with parentheses, we move on to exponents and roots!
Pay attention - even within parentheses, it's very important to maintain the correct order of operations!
Exponent - multiply the base by itself the number of times shown in the exponent (the small number on the top right).
Root - half power - which positive number when multiplied by itself will give the number written under the root.
Practice Powers and Roots
Test your knowledge with 24 quizzes
\( 10:2-2^2= \)
Examples with solutions for Powers and Roots
Step-by-step solutions included
Exercise #1
Step-by-Step Solution
First, compute the power: .
Next, divide: .
Finally, subtract: .
Answer:
Exercise #2
Step-by-Step Solution
First, compute the power: .
Next, divide: .
Finally, subtract: .
Answer:
Exercise #3
Step-by-Step Solution
First, compute the power: .
Next, divide: .
Finally, subtract: .
Answer:
Exercise #4
Step-by-Step Solution
First, evaluate the square root: .
Then, follow the order of operations (PEMDAS/BODMAS):
1. Multiplication:
2. Subtraction:
So, the correct answer is .
Answer:
Exercise #5
Step-by-Step Solution
First, evaluate the square root: .
Then, follow the order of operations (PEMDAS/BODMAS):
1. Addition:
2. Subtraction:
So, the correct answer is .
Answer:
Frequently Asked Questions
What comes first in order of operations: exponents or multiplication?
+Exponents come before multiplication in the order of operations (PEMDAS/BODMAS). After handling parentheses, you solve all exponents and roots first, then move to multiplication and division from left to right.
How do you solve square roots in order of operations problems?
+Square roots are solved in the second step of PEMDAS, right after parentheses and alongside exponents. Calculate the square root value first, then continue with multiplication, division, addition, and subtraction in order.
What does any number to the power of 0 equal?
+Any number raised to the power of 0 equals 1, regardless of the base number. For example: 5⁰ = 1, 100⁰ = 1, and even 1230⁰ = 1. This is a fundamental exponent rule.
Do you solve exponents and roots from left to right?
+Unlike multiplication/division and addition/subtraction, the order of solving exponents and roots doesn't matter as long as you solve them all before moving to the next step. You can work from left to right or tackle them in any order.
How do you handle exponents inside parentheses?
+When exponents appear inside parentheses, follow the complete order of operations within the parentheses first. Solve exponents and roots inside the parentheses, then complete any remaining operations before removing the parentheses.
What are the basic square root formulas I need to know?
+Key square root formulas include: √(a×b) = √a × √b for products, √(a/b) = √a / √b for quotients, and ⁿ√ᵐ√a = ⁿᵐ√a for nested roots. These help simplify complex root expressions.
Why do order of operations rules matter in math?
+Order of operations ensures everyone gets the same answer when solving mathematical expressions. Without these rules (PEMDAS), expressions like 4² - √25 + 10 could be interpreted multiple ways, leading to different incorrect answers.
What's the difference between 2³ and 3²?
+2³ means 2 × 2 × 2 = 8 (multiply 2 by itself 3 times), while 3² means 3 × 3 = 9 (multiply 3 by itself 2 times). The base number and exponent position determine the calculation method and final result.