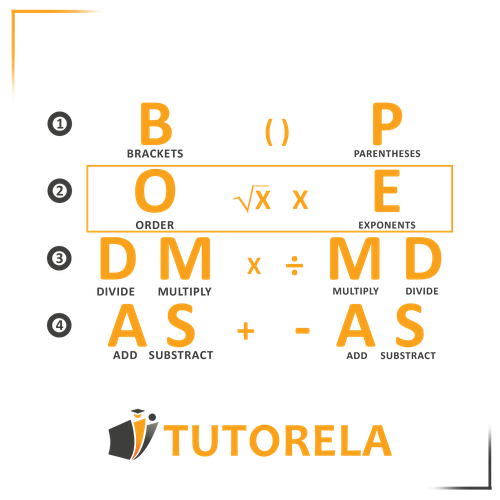
As we have learned in previous lessons, when working with combined operations the order of the basic operations must be followed in order to get the correct result. However, before performing these the parentheses and then the roots and powers must first be solved.
Roots are very important in mathematical calculations. They are present in a variety of exercises ranging from algebraic problems for solving a second degree equation using the general formula, to geometric problems like determining the length of the hypotenuse of a right-angled triangle. Therefore, it is fundamental that we learn how to solve combined operations where this operation appears.
When we have simplified the root and power operations, we can continue solving the exercise according to the order of the basic operations: multiplications and divisions first, followed by additions and subtractions.
Let's revisit the order of the operations: