Order of Operations: (Exponents) - Examples, Exercises and Solutions

The given mathematical expression is $10:2-2^2$.

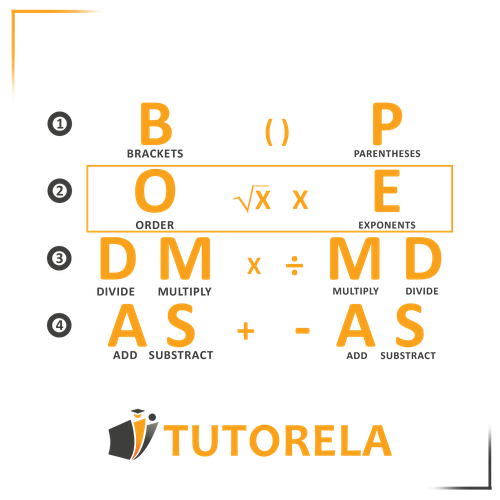
According to the order of operations (often remembered by the acronym PEMDAS/BODMAS), we perform calculations in the following sequence:

• Parentheses/Brackets
• Exponents/Orders (i.e., powers and roots)
• Multiplication and Division (from left to right)
• Addition and Subtraction (from left to right)

In this expression, there are no parentheses, but there is an exponent: $2^2$. We calculate the exponent first:

$2^2 = 4$

Substituting back into the expression, we have:

$10:2-4$

Next, we perform the division from left to right. Here, ":" is interpreted as division:

$10 \div 2 = 5$

Now, substitute this back into the expression:

$5 - 4$

The final step is to perform the subtraction:

$5 - 4 = 1$

Therefore, the answer is $1$.

First, compute the power: $5^2 = 25$.

Next, divide: $25 \div 5 = 5$.

Finally, subtract: $10 - 5 = 5$.

First, compute the power: $4^2 = 16$.

Next, divide: $16 \div 2 = 8$.

Finally, subtract: $15 - 8 = 7$.

First, compute the power: $3^3 = 27$.

Next, divide: $27 \div 3 = 9$.

Finally, subtract: $20 - 9 = 11$.

First, evaluate the square root: $\sqrt{81}=9$.

Then, follow the order of operations (PEMDAS/BODMAS):

1. Multiplication: $3 \times 2 = 6$

2. Addition: $6 + 9 = 15$

So, the correct answer is $15$.

First we need to remind ourselves of the order of operations:

1. Parentheses

2. Exponents and Roots

3. Multiplication and Division

4. Addition and Subtraction

There are no parentheses in this problem, therefore we will start with exponents:

3 * 3 + 3² =

3 * 3 + 9 =

Let's continue to the next step—multiplication operations:

3 * 3 + 9 =

9 + 9 =

Finally, we are left with a simple addition exercise:

9 + 9 = 18

To solve the expression $4 + 2^2$, follow the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)).

Let's break down the expression:

• Step 1: Identify any exponents.
  The expression contains an exponent: $2^2$. To evaluate this, multiply 2 by itself: $2 \times 2$, which equals 4.
  So, $2^2 = 4$.
• Step 2: Perform addition.
  Now, substitute the result back into the original expression:
  $4 + 4$.
  Add these numbers together: 4 + 4 equals 8.

Therefore, the answer to the expression $4 + 2^2$ is 8.

To solve the expression $4 + 2 + 5^2$, we need to follow the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).

• Step 1: Calculate Exponents
  In the expression we have an exponent: $5^2$. This means 5 is raised to the power of 2. We calculate this first:
  $5^2 = 25$.


• Step 2: Perform Addition
  Now, substitute the calculated value back into the expression:
  $4 + 2 + 25$.
  Perform the additions from left to right:
  $4 + 2 = 6$
  Finally add the result to 25:
  $6 + 25 = 31$.

First, solve the square root: $\sqrt{49} = 7$.

Next, multiply 7 by 3: $7 \times 3 = 21$.

Finally, add 4 to 21: $4 + 21 = 25$.

Start by calculating the power: $5^2 = 25$.

Then, calculate the square root: $\sqrt{16} = 4$.

Subtract 4 from 25: $25 - 4 = 21$.

Finally, add 2: $21 + 2 = 23$.

To solve the expression $5+\sqrt{36}-1=$, we need to follow the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).

Here are the steps:

First, calculate the square root:

$\sqrt{36} = 6$

Substitute the square root back into the expression:

$5 + 6 - 1$

Next, perform the addition and subtraction from left to right:

Add 5 and 6:

$5 + 6 = 11$

Then subtract 1:

$11 - 1 = 10$

Finally, you obtain the solution:

$10$

First, follow the order of operations (BODMAS/BIDMAS):

Step 1: Calculate the exponent:
$2^2 = 4$

Step 2: Perform the multiplication:
$5 \times 4 = 20$

Step 3: Perform the addition and subtraction from left to right:
$6 - 3 + 20 = 23$

The correct result is: $23$.

To solve the expression $6+\sqrt{64}-4=$, we need to follow the order of operations (PEMDAS/BODMAS):

• P: Parentheses (or Brackets)
• E: Exponents (or Orders, i.e., powers and roots, etc.)
• MD: Multiplication and Division (left-to-right)
• AS: Addition and Subtraction (left-to-right)

In this expression, we first need to evaluate the square root since it falls under the exponent category:

$\sqrt{64} = 8$

Next, we substitute the computed value back into the expression:

$6+8-4$

We then perform the addition and subtraction from left to right:

$6+8 = 14$

$14-4 = 10$

Thus, the final answer is:

$10$

First, evaluate the square root: $\sqrt{49}=7$.

Then, follow the order of operations (PEMDAS/BODMAS):

1. Addition: $7 + 7 = 14$

2. Subtraction: $14 - 5 = 9$

So, the correct answer is $9$.

Let's solve the expression step by step using the order of operations, often remembered by the acronym PEMDAS, which stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).

The given expression is: $8-3^2:3=$

Step 1: Evaluate Exponents
The expression has an exponent, which we need to evaluate first. The exponent is $3^2$.
Calculate $3^2$ which equals $9$.
Now the expression becomes: $8 - 9 : 3$

Step 2: Division
Next, perform the division operation. Here we divide $9$ by $3$.
Calculate $9 : 3$ which equals $3$.
Now the expression becomes: $8 - 3$

Step 3: Subtraction
Finally, perform the subtraction.
Calculate $8 - 3$ which equals $5$.

Therefore, the solution to the expression $8-3^2:3$ is $5$.