Order of Operations with Parentheses Practice Problems

Master PEMDAS/BODMAS rules with step-by-step parentheses practice problems. Solve advanced order of operations exercises with confidence using proper mathematical sequence.

📚Practice Solving Order of Operations with Parentheses
  • Solve multi-step expressions by identifying and evaluating parentheses first
  • Apply PEMDAS/BODMAS rules correctly in complex mathematical expressions with grouping symbols
  • Master the sequence: parentheses, exponents, multiplication/division, addition/subtraction from left to right
  • Work through expressions containing multiple operations including division, multiplication, and parentheses
  • Build confidence solving real-world math problems requiring proper order of operations
  • Develop systematic problem-solving approach for advanced arithmetic expressions

Understanding Parentheses in advanced Order of Operations

Complete explanation with examples

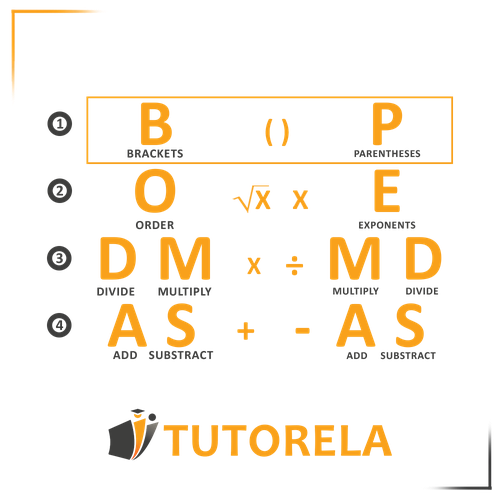
In previous articles, we have seen what is the order of operations for addition, subtraction, multiplication, and division and also the order we must follow when there are exponents.

When the exercise we need to solve includes parentheses, we always (always!) start with the operation contained within them.

  1. Parentheses
  2. Exponents and roots
  3. Multiplications and divisions
  4. Additions and subtractions

Reminder: when an exercise presents operations that have the same precedence, that is, multiplications and divisions or additions and subtractions, we will solve the exercise from left to right.

Visual representation of BODMAS/PEMDAS rule emphasizing Brackets (Parentheses) as the first step in arithmetic problem-solving, crucial for accurate mathematical operations

Detailed explanation

Practice Parentheses in advanced Order of Operations

Test your knowledge with 27 quizzes

\( 20\div(4+1)-3= \)

Examples with solutions for Parentheses in advanced Order of Operations

Step-by-step solutions included
Exercise #1

(7+2)×(3+8)= (7+2)\times(3+8)=

Step-by-Step Solution

Simplify this expression paying attention to the order of operations. Whereby exponentiation precedes multiplication, division precedes addition and subtraction and that parentheses precede all of the above.

Therefore, let's first start by simplifying the expressions within the parentheses. After which we perform the multiplication between them:

(7+2)⋅(3+8)=9⋅11=99 (7+2)\cdot(3+8)= \\ 9\cdot11=\\ 99 Therefore, the correct answer is option B.

Answer:

99

Video Solution
Exercise #2

8×(5×1)= 8\times(5\times1)=

Step-by-Step Solution

According to the order of operations, we first solve the expression in parentheses:

5×1=5 5\times1=5

Now we multiply:

8×5=40 8\times5=40

Answer:

40

Video Solution
Exercise #3

(2+1×2)2= (2+1\times2)^2=

Step-by-Step Solution

Let's solve the expression (2+1×2)2 (2+1\times2)^2 step-by-step, adhering to the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)).

Firstly, handle the expression inside the parentheses (2+1×2) (2+1\times2) :

  • Within the parentheses, according to PEMDAS, we first perform the multiplication 1×21\times2 which equals 22.
  • Now, the expression inside the parentheses becomes (2+2) (2+2) .
  • Next, perform the addition: 2+2=42+2=4.

Now the expression simplifies to 424^2.

Second, handle the exponent:

  • Calculate the square of 4: 42=164^2 = 16.

Thus, the final answer is 1616.

Answer:

16

Video Solution
Exercise #4

Solve the following equation:

18−(3+3)= 18-(3+3)=

Step-by-Step Solution

Let's begin by simplifying the expression following the order of operations.

P- PARENTHESES

E-EXPONENTS

D-DIVISION

A-ADDITION

S-SUBTRACTION

18−(3+3)=18−6=12 18-(3+3)= \\ 18-6= \\ 12

Therefore the correct answer is answer D.

Answer:

12

Video Solution
Exercise #5

10−(10−4):2= 10-(10-4):2=

Step-by-Step Solution

Let's simplify this expression while following the order of operations which states that exponents come before multiplication and division, which come before addition and subtraction, and that parentheses come before all of them,

We will start by simplifying the expression inside the parentheses and calculate the result of the subtraction within them, then - since division comes before subtraction, we will first perform the division operation and then perform the subtraction operation:

10−(10−4):2=10−6:2=10−3=7 10-(10-4):2= \\ 10-6:2= \\ 10-3= \\ 7

Therefore, the correct answer is answer B.

Answer:

7

Video Solution

Frequently Asked Questions

Everything you need to know about Parentheses in advanced Order of Operations

What is the correct order of operations with parentheses?

+
The correct order is PEMDAS/BODMAS: 1) Parentheses/Brackets first, 2) Exponents/Orders, 3) Multiplication and Division (left to right), 4) Addition and Subtraction (left to right). Always solve what's inside parentheses before any other operations.

Why do parentheses come first in order of operations?

+
Parentheses indicate grouping and show which operations should be performed together first. They override the normal order of operations, ensuring mathematical expressions are solved correctly and consistently across all problems.

How do you solve 4+(6÷2) step by step?

+
Step 1: Solve inside parentheses first: 6÷2 = 3. Step 2: Replace the parentheses with the result: 4+3. Step 3: Perform addition: 4+3 = 7. The final answer is 7.

What happens when there are multiple parentheses in one problem?

+
Solve each set of parentheses separately first, then continue with the remaining operations following PEMDAS/BODMAS order. For example, in (21+3)×2×4-(22÷2), solve both (21+3)=24 and (22÷2)=11 first, then proceed with multiplication and subtraction.

Do you multiply or divide first when they're in the same problem?

+
When multiplication and division appear together, work from left to right in the order they appear. They have equal precedence, so the left-to-right rule applies after solving any parentheses and exponents first.

How do you remember the order of operations with parentheses?

+
Use memory aids like PEMDAS (Please Excuse My Dear Aunt Sally) or BODMAS (Brackets, Orders, Division/Multiplication, Addition/Subtraction). The key is remembering parentheses/brackets always come first, then follow the sequence systematically.

What are common mistakes students make with parentheses in order of operations?

+
Common errors include: 1) Not solving parentheses first, 2) Working left to right without following PEMDAS, 3) Forgetting that multiplication and division have equal priority, 4) Not properly handling multiple sets of parentheses. Always identify and solve all parentheses before proceeding.

Can you have parentheses inside parentheses in math problems?

+
Yes, nested parentheses are common in advanced problems. Solve the innermost parentheses first, then work outward. For complex expressions, you might also see brackets [ ] and braces { } to show different levels of grouping.

More Parentheses in advanced Order of Operations Questions

Click on any question to see the complete solution with step-by-step explanations

Parentheses in advanced Order of Operations

Solve 20·4:5·(3+0·7-1): Order of Operations Practice Solve: 2(3 + ½×8) - Order of Operations with Mixed Numbers Solve the Expression: 6·(3+5·2-13) Using Order of Operations Solve (3·5+5)÷(4+3·2): Order of Operations Practice Solve 4+(6+6÷3)×2: Order of Operations Practice

Continue Your Math Journey

Master Parentheses in advanced Order of Operations first, then advance to these related topics that build on your fraction skills

Suggested Topics to Practice in Advance

The Order of Basic Operations: Addition, Subtraction, and MultiplicationOrder of Operations: ExponentsOrder of Operations: RootsOrder of Operations - Exponents and Roots

Topics Learned in Later Sections

Division and Fraction Bars (Vinculum)The Numbers 0 and 1 in OperationsNeutral Element (Identity Element)Order or Hierarchy of Operations with FractionsMultiplicative InverseSpecial cases (0 and 1, reciprocals, fraction line)The Order of Operations

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Addition, subtraction, multiplication and division Exercises with fractions Identify the greater value Only addition and subtraction Parentheses within parentheses Solving an exercise Solving the problem True / false Using 0 Using fractions Using negative numbers Using parentheses Using variables