Exponential Equations

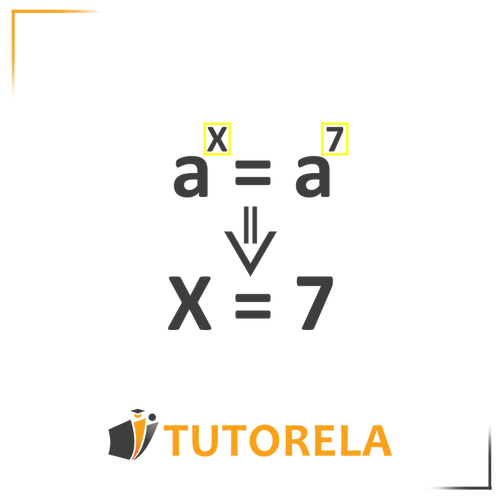
The method is based on the principle that says when 
$a^x=a^y$
Then 
$x=y$

That is, if we reach a situation where the bases are identical, we can easily compare the powers and find the unknown we are looking for.
If we could not get to the same bases, we will move on to the second method:

In this method, we use substitution to replace elements that are cumbersome to work with, with elements we know how to handle.
For this method to work, we must bring the function to a specific form.
We will have to bring our exercise to a state where there is an element, the same quadratic element, and a free number (without variables).
Once we reach this state, we will use a power player $t$ and place it in place of the element we have with a variable power.
Thus, we will arrive at a common quadratic equation that we can easily solve.

If we could not obtain the same bases, we will resort to the second method:
Solving exponential equations using a quadratic equation and placing $t$

Thus, we will have to bring our exercise to a state in which there is an element, the same squared, and a free number (without variable).
$(A^x )^2+B\times A^x+C=0$
Once we reach this state, we will use a booster player $t$ and place it in place of the element we have with a variable power.
$t^2+Bt+C=0$
In this way, we will obtain a standard quadratic equation that we can easily solve.
Important! The solution of the quadratic equation is not the final result of the exercise.
We will not forget to place the values of the $t$ we found to find the variable values we are looking for $x$.

How do we reach a point where there are identical bases? We will break down the numbers correctly into prime factors.

For example:
$8^x=2^{x+2}$

We can break $8$ down into factors and thus obtain that:
$8=2^3$
therefore:
$(2^3 )^x=2^{x+2}$

According to the properties of powers we obtain that:
$2^{x+2}=2^{3x}$

We have reached a point where the bases are identical! Now we can compare the powers and find the $X$.

$3x=x+2$
$2x=2$
$x=1$

To bring the equation to a state where there is one element, the same element squared, and a free number, we will need to use the properties of powers.
We will remember the following power rules:

$(a^n )^m=a^{n\times m}$

$a^{n+m}=a^n\times a^m$

Let's take the following example:
$4^{2x}+4^{x+1}=0$
To bring the equation to a state where there is one element, the same element squared, and a free number, we will have to use power rules.
According to the power laws, we can say that:
$4^{2x}=(4^x)^2$
In fact, we isolated $4^x$ and showed that it was quadratic.

We will also take $4^{x+1}$
According to the power laws, it can be said that:
$4^{x+1}=4\times 4^x$

Now, let's rewrite the same equation with the data we received and we get:
$(4^x )^2+4\times 4^x=0$

Now, we place $t$ in place of the element with an unknown power.
Let's say that: $t=4^x$
Every time we use $4^x$ we replace it with, $t$
Now, our equation will be simpler and will look like this:

$t^2+4\times t=0$
In fact, we have a simple quadratic equation!
Solve and find that:
$t^2+4t=0$
$t=-4, t= 0$

Pay attention!! This is not our final answer!
We have found the $t$ and not the unknown we are looking for $X$.
To find $x$ we place in the equation $t=4^x$ the results we obtained.
Attention! Both solutions were rejected because the power for a number that is not $0$ cannot be $0$.
The second solution is $-4$ disqualified because a power for a positive number always yields a positive result.

Therefore, there is no result!

If you found this article interesting, you might also be interested in the following articles:

• First-degree equations with one unknown
• What is the unknown in a mathematical equation?
• Equivalent equations
• Transposition of terms
• Solving equations by adding or subtracting the same number from both sides
• Solving equations by multiplying or dividing both sides by the same number
• Solving equations by simplifying like terms
• Solution of an equation

In the blog of Tutorela you will find a variety of articles about mathematics.