Long Division

Long division is a method used to divide large numbers by breaking down the process into a series of easier steps, dealing with one digit at a time. This technique is especially useful for dividing numbers that don’t divide evenly.

How to use Long Division?

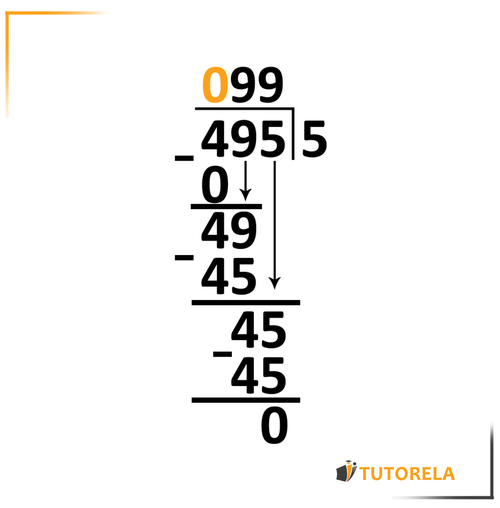
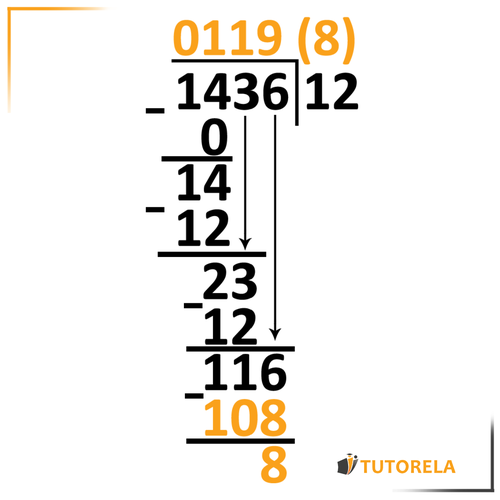
We'll go step by step, dividing one digit at each step. We'll start with the digit on the left, write down the division result above the drawn line, and look for the remainder.
To do so, follow these steps:

Divide: Determine how many times the divisor fits into the first few digits of the dividend.
Multiply: Multiply the divisor by the quotient found in the first step and write the result under the dividend.
Subtract: Subtract the result from the dividend to find the remainder.
Bring Down: Bring down the next digit of the dividend and repeat the process.
Repeat: Continue until all digits have been brought down and divided, resulting in a final quotient and possibly a remainder.

Long Division Notation

In long division, the notation is set up to clearly show the process of dividing step-by-step. The main elements include:

Dividend: The number being divided. It is placed inside the long division symbol (also known as the “division bracket”).
Divisor: The number by which you are dividing. This is placed outside the division bracket, on the left.
Quotient: The result of the division. It is written on top of the division bracket, directly above each respective digit of the dividend as each part of the division is solved.
Remainder: If the divisor does not divide the dividend evenly, you may have a remainder. This remainder is written after the quotient or represented as a decimal or fraction.

The division bracket helps structure the process, allowing you to handle one digit of the dividend at a time. As you solve each step, you bring down the next digit from the dividend, repeating the process until no digits remain. If there’s a remainder that does not go evenly into the divisor, it can be expressed next to the quotient or as a decimal by adding a zero and continuing the division process.

Detailed explanation

Start practice

Test yourself on long division!

Practice more now

Long Division

Notation Mode

We'll draw a division bar
Inside the bar, we'll write the dividend (the number we want to divide).
To its left, we'll write the divisor (the number by which we want to divide).
Above the bar, we'll write the quotient (the result of the division).
In each step, we will divide one digit. We start with the leftmost digit, write the result (whole numbers only) above the bar, and look for the remainder by multiplying this number by the divisor.
We write the result of the multiplication below the number we just divided and subtract to find the remainder.
We bring down the next digit from above to continue dividing.
We divide in the same way, find the remainder.
When there are no more digits to bring down, it means we have finished the exercise.
The digit that we cannot divide is the remainder or residue.

Division of a Two-Digit Number by a Single-Digit Number

Take a look at the following exercise: $93:3=$
Solution:

Division of a two-digit number by a one-digit number

We will set it up this way:
Write the dividend inside the bar. To its left, write the divisor.
Above the bar, we will write the quotient.
Pay attention: What matters to us in this exercise are the quotient and the remainder.
First, we will divide the first digit $9$ by the number $3$ .
We'll record the result above the digit $9$ on the bar.
$9:3=3$

$3$ is the quotient.

2 - Division of a two-digit number by a one-digit number

Remember that we said we're also interested in the remainder?
To find it, we'll multiply the $3$ (the result we obtained) by $3$ (the divisor).
Record the result below the $9$ .
$3 × 3=9$

Now, we subtract $9$ from $9$ and we get the remainder.
$9-9=0$
We obtained a remainder of $0$

Now let's move on to the second digit $3$ .
We bring it down from the top and divide the number again.
$3:3=1$
The quotient is $1$ , so we will write it above the digit $3$ on the bar.
Let's see what the remainder is:
Multiply the quotient by the divisor, it will give us
$1×3=3$
Write $3$ below $3$ and subtract.

3 - Division of a two-digit number by a one-digit number

We will get a remainder of $0$ . There is no remainder, and we don't have any more digits to bring down, which means we are finished.
The quotient is what remains written above the bar: $31$

4 - Division of a two-digit number by a one-digit number

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Question 2

Question 3

Division of a Three-Digit Number by a One-Digit Number

Look at the following exercise:
$644:4=$
Solution:
We will write it out correctly.

Now we will divide the digit located on the left $6$ .
We will write the result above the bar, only the whole numbers.

$6:4=1$
Plus the remainder.
Let's write $1$ above the bar on top of the number $6$ .

2 - Division of a three-digit number by a one-digit number

Now let's find the remainder: multiply the result $1$ by the divisor $4$ and subtract as needed.

The remainder is $2$ .
Let's bring down the next digit.
Now we have a completely new number $24$

3 - Division of a three-digit number by a single-digit number

We will divide $24$ by $4$ .
$24 ÷ 4 = 6$
Write down the $6$ above the digit $4$ over the bar.
We will find the remainder by multiplying by the divisor and subtracting accordingly:

4 - Division of a three-digit number by a single-digit number

We got the remainder $0$ .
Now let's move on to the third digit $4$ .
We bring it down from above
and divide:
$4:4=1$
Let's write $1$ above the bar in the correct place.
The remainder is $0$ .
We have completed the exercise and the result is $161$ .

Step 5 -Dividing a three-digit number by a one-digit number

Note:
If we had received an exercise like this:

When dividing $4$ by $5$ , it turns out that there are no whole numbers because $4$ is smaller than $5$ .
Therefore, in a case like this, you would write $0$ over $4$ , continue to find the remainder, and proceed in the same manner.
Bring down the number $9$ and so on.
The answer is $99$ .

Division by a Two-Digit Number

Look at the exercise $1436 \div 12=$
Solution:
We will write it down correctly.
We notice that the number $1$ is less than $12$ , so we write a $0$ above the number $1$ .
Let's find the remainder $14$ .
Divide $14$ by $12$ and we get $1$ .
Let's find the remainder and proceed in the same manner.
The answer is $119$ and the remainder is $8$ .