We will perform the same multiplication operation on the numerator and the denominator: the value of the fraction will be preserved.
You can expand as many times as you want and by any number.
We will perform the same multiplication operation on the numerator and the denominator: the value of the fraction will be preserved.
You can expand as many times as you want and by any number.
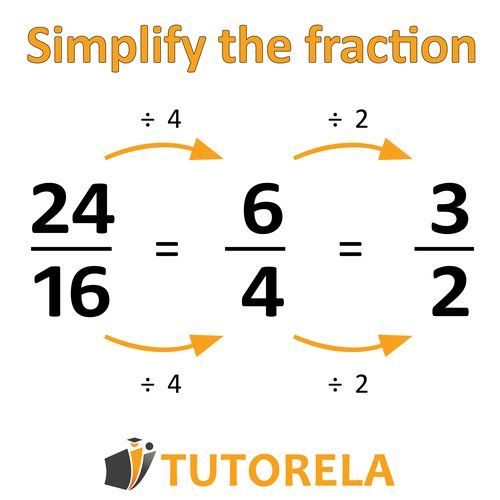
We will perform the same division operation on the numerator and the denominator: the value of the fraction will be preserved.
This can only be done with a number that is completely divisible by both the numerator and the denominator.
It is possible to simplify only until reaching a fraction in which it is not possible to find a number that divides without remainder both in the numerator and the denominator.
Simplify the following fraction:
\( \frac{16}{8}= \)
Simplifying and amplifying fractions is an easy and enjoyable topic that will accompany you in almost all exercises with fractions.
Simplifying and amplifying a fraction is actually a multiplication or division operation that is performed on the fraction so that the real value of the fraction does not change and simply looks different.
Expansion: a multiplication operation (which is performed on both the numerator and the denominator).
Simplification: a division operation (which is performed on both the numerator and the denominator).
Think of a pizza with slices: a normal family-sized pizza sold at pizzerias.
You call to place the order and ask the seller to put olives on half of the pizza.

You will receive pizza with olives.
But, what if you told the seller, please put olives on triangles of the pizza?
Let's see:
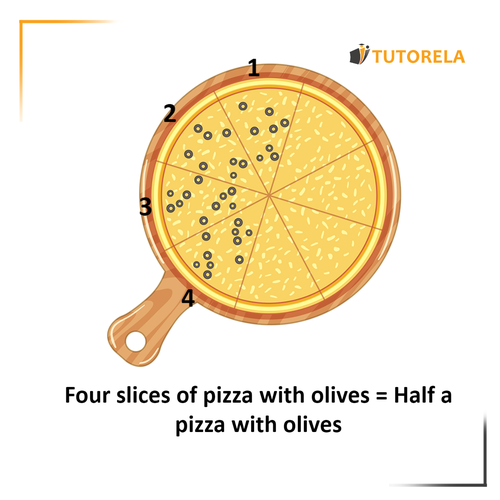
Even then you would get half a pizza with olives.
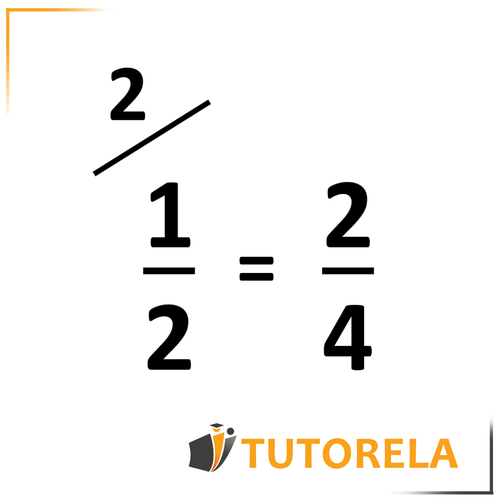
That is to say: -> four slices out of is equal to
Now let's see this in the exercise
We expand the fraction by
Solution:
We multiply by both in the numerator and the denominator and we get:
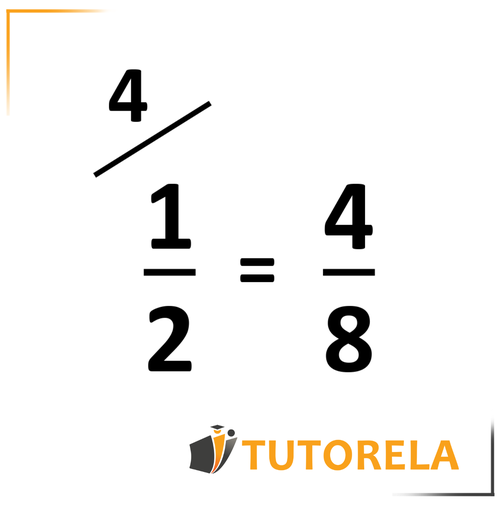
Note the sign that is usually used to expand.
If we multiply both the numerator and the denominator by the same number, the value of the fraction will not change and the fractions will be equal, exactly as in the pizza.
Important note: we can expand the fraction as many times as we want and by any number we want and still the value will not change!
For example, even if instead of being expanded by we would expand by , we would get:
which is also equal to
Complete the missing number
Solution:
We see that in the numerator becomes . That is, it is multiplied by . Therefore, we also multiply the denominator by the number to reach the correct result.
After all, we learned that fractions will be equal only if we perform the operation on both the numerator and the denominator.
We obtain:
Simplify the following fraction:
\( \frac{1}{1}= \)
Simplify the following fraction:
\( \frac{2}{10}= \)
Simplify the following fraction:
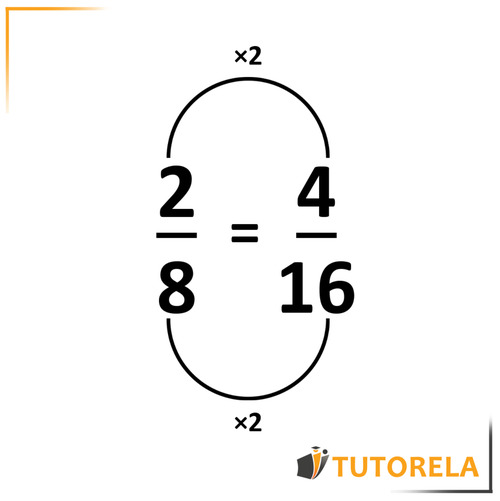
\( \frac{4}{16}= \)
Simplifying fractions is a division operation that is performed on both the numerator and the denominator and preserves the value of the fraction.
It is possible to simplify only by a number that is divisible without remainder in both the numerator and the denominator.
When can we not simplify a fraction?
When the numerator and the denominator are not completely divisible by the same number.
Simplify the fraction by .
Solution:
We divide both the numerator and the denominator by and we get:
Extra section:
We simplify the fraction by the number you choose (except for )
Solution:
We must choose a number that divides both the numerator and the denominator without remainder.
We are asked: What number can you divide and by?
The answer can be: or . For example
We choose: and simplify:
We simplify the fraction:
Solution:
This exercise has no solution. This fraction cannot be simplified further since there is no number that is divisible by and also by without a remainder.
Complete the missing number
Solution:
We see that in the numerator becomes . That is, it is divided by . Therefore, we also divide in the denominator by the number to arrive at the correct result since we learned that fractions will be equal only if we perform the operation both in the numerator and in the denominator.
We obtain:
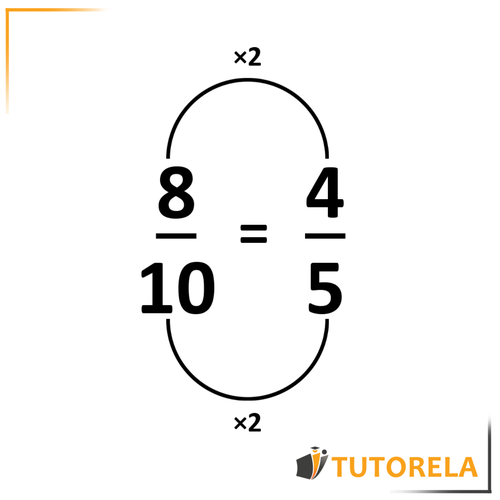
Note: Expansion does not mean that the fraction gets bigger and simplification does not mean that the fraction gets smaller!
Simplify the following fraction:
Let's simplify as follows, we'll divide both the numerator by 2 and the denominator by 2:
Simplify the following fraction:
Let's reduce as follows, we'll divide both the numerator and denominator by 1:
Simplify the following fraction:
Let's simplify as follows, we'll divide both the numerator by 2 and the denominator by 2:
Simplify the following fraction:
We will reduce in the following way, divide the numerator by 4 and the denominator by 4:
Simplify the following fraction:
Let's reduce as follows, divide the numerator by 4 and the denominator by 4:
Simplify the following fraction:
\( \frac{12}{4}= \)
Simplify the following fraction by a factor of 1:
\( \frac{3}{10}= \)
Simplify the following fraction by a factor of 3:
\( \frac{3}{6}= \)