Hundredths and Thousandths

In this article, we will learn about hundredths and thousandths and learn everything necessary about them.

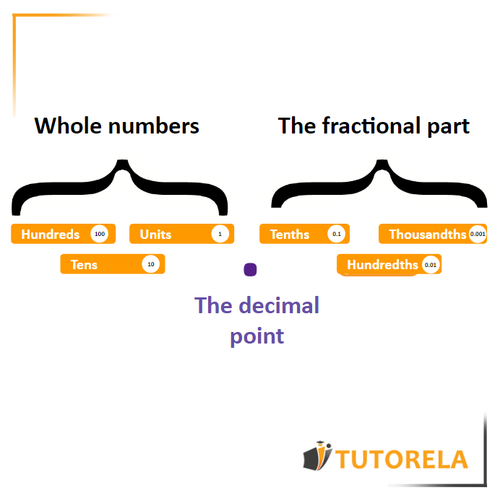
First, let's remember the structure of the decimal number:

A hundredth is a part of a whole divided into $100$ equal parts.

To deeply understand what a hundredth is, let's think of an example from life:

Let's think about a birthday cake that is on the festive table.
At the party, there are $100$ guests.

If the cake is divided into equal parts among everyone, so that everyone gets an equal part of the cake, each guest will receive a hundredth of the cake.

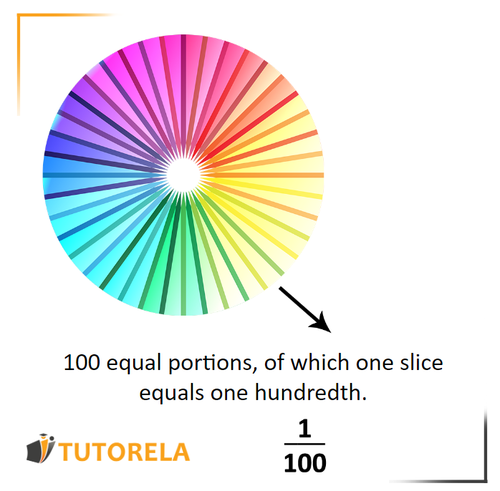
In fact, a portion of $100$ or in fraction $1 \over 100$

If we look above, in the structure of the decimal fraction we see that the hundredths are in the second place to the right of the decimal point and represent a fraction whose denominator is $100$.

What will happen if we tell you that only $5$ guests ate the cake, each one a slice?

In reality, only $5$ portions of $100$ were eaten, that is, $5 \over 100$,$5$ hundredths.

If we want to convert it to a decimal number we get:

$0.05$
Explanation:

There are $0$ wholes –> there are no wholes in the fraction
We add a decimal point

Tenths, we don't have them, so it will be $0$ hundredths –> $5$ hundredths.

Extra section:

What would happen if $17$ portions were eaten?

In fact, $17\over 100$ ->  $17$ hundredths? 
How would we pronounce the hundredths as a decimal number?$17$

Solution:

As $17$ is made up of $10$ and another $7$
That is, one tenth and another $7$ hundredths 
Therefore: $0.17$

How many hundredths are there in the number $2.56$?
Solution:
There are $6$ hundredths in the number.
We learned that the hundredth digit is the second to the right of the decimal point.
Firstly -> the number $5$ represents the tenths.

And secondly, the number $6$ represents the hundredths.

We place the decimal point so that $8$ is the hundredths digit in the number.
$54689$

Solution:

$54.689$
We place the decimal point so that the number $8$ is $2$ steps from it to the right.
When the digit is in the second place from the right $2$ steps expresses the hundredths.

A thousandth is a part of a whole that is divided into $1000$ equal parts. If we divide a cake into $1000$ equal parts and eat one portion -> we actually ate a thousandth of the cake -> $1 \over 1000$

In the structure of the decimal fraction, it seems that thousandths are in the third place to the right of the decimal point and represent a fraction whose denominator is $1000$.

What is the thousandths digit in the number $8.672$?

Solution:

The thousandths digit is $2$ -> the digit that is in the third place to the right of the decimal point.

A large group of ants found $1000$ marshmallow crumbs of the same size.

Surprisingly, only $700$ ants tasted the marshmallow, each one tasted one crumb.

How many marshmallows were eaten?

Solution:

$700 \over 1000$
Were eaten $700$ thousandths –> $700$ equal crumbs of $1000$ which are also$0.700$