To locate fractions on the number line, we will carry out several steps.
Placing Fractions on the Number Line
Placing Fractions on the Number Line
First Step – Discovering the Value of Arcs
We will subtract two given numbers and keep the difference.
We will count the number of arcs between the numbers.
We will divide the subtraction result by the number of arcs to find out the measure of each arc.
Step Two – Placing the Numbers on the Number Line
Depending on the amount of arcs, the scale can be expanded or reduced.
Test yourself on fractions on a number line!
What are the missing numbers (?) on the numer line below?
Fractions on the Number Line
In this article, we'll learn how to order fractions on the number line with ease, speed, and without any trouble.
Let's first look at the number line and analyze it.
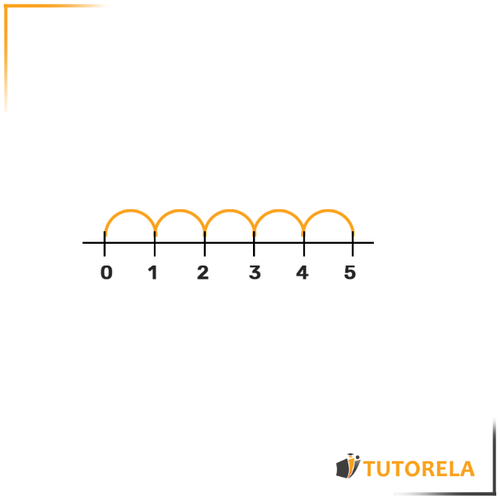
Here we see a number line from to .
We notice that the line is divided into sections, and each mark indicates an increase of .
However, if we look at this number line:
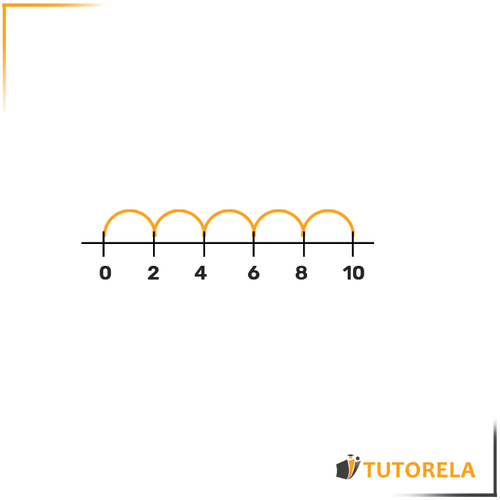
We'll see that each mark indicates an increase of .
To place fractions on the number line, the first thing we need to understand is how much we increase from one segment to the next.
The lines that mark the end of each segment on the number line are called points. It is also common to say that – represents the space between the two points.
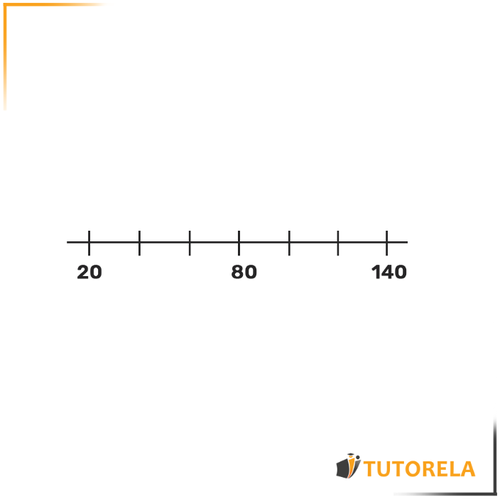
Exercise Practice
Complete the missing numbers on the number line:
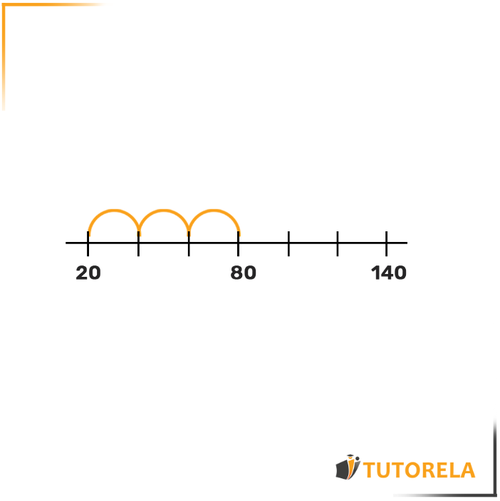
Solution:
To fill in the numbers, first let's mark, with an arc, the spaces that are between the dots of the two given numbers.
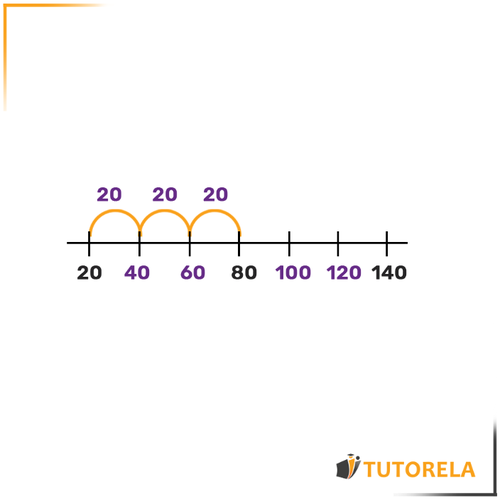
We will notice that there are arcs between the number and .
Remember, all the spaces are identical.
Let's subtract .
is the total space.
Since there are arcs, we will divide the by to find the measure of each arc.
We will find that:
Therefore, each arc measures .
We will place marks on the number line so we can easily fill in the remaining numbers:
Now that we know a bit more about the number line and have learned how to find the distance between two points, we can move forward.
What number is missing (?) from the number line?
What number is missing (?) on the number line below?
What number is missing (?) from the number line below?
Fractions on the Number Line
First Step
Finding the Measure of the Arc Between Two Points in the Following Way:
Subtract the two given numbers and keep the difference.
Count the number of arcs that are between the numbers.
Divide the result of the subtraction by the number of arcs to find out the measure of each arc.
Second step
Placing the Numbers: Reduction and expansion can be applied if necessary.
Let's continue learning with an example
Put the fractions and on the number line.
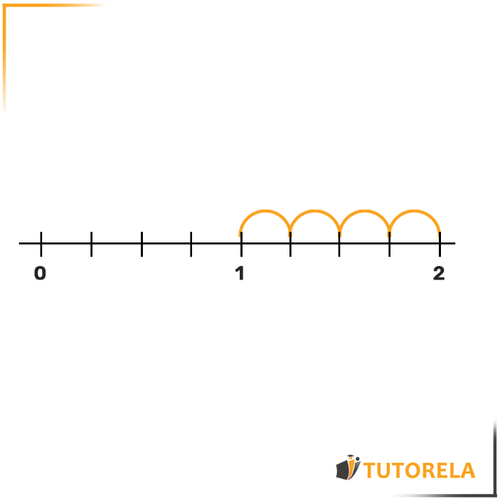
Let's ask ourselves, what is the difference between the given numbers?
For example, between and ?
The difference is .
How many arcs are there between and ?
arcs.
We will divide the difference we calculated by the number of arcs and we will get:
Each arc measures .
Now let's think about where to place the .
We can scale up the by and we get .
Therefore, will be placed here:
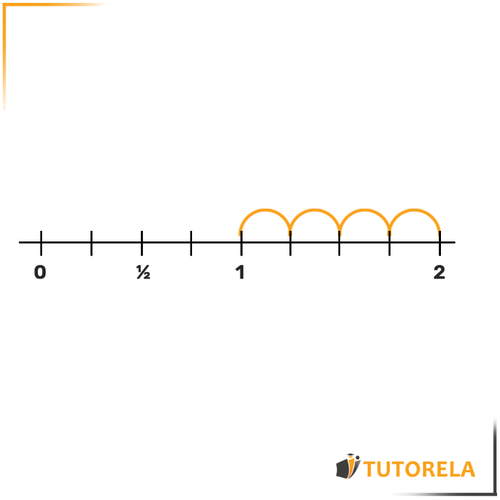
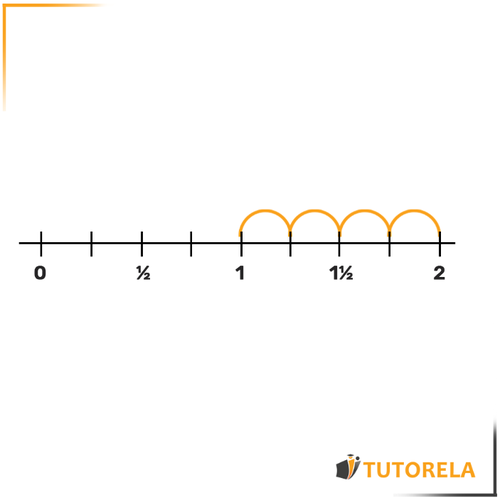
Now let's move on to
We see that there is a whole number 1 in the fraction, so it will be located between and
We saw that each segment measures and deduced that is equivalent to .
Therefore, will be located here:
What is the missing number (?) on the number line below?
What is the missing number (?) marked on the number line below?
What number is missing (?) from the number line below?
Another Exercise
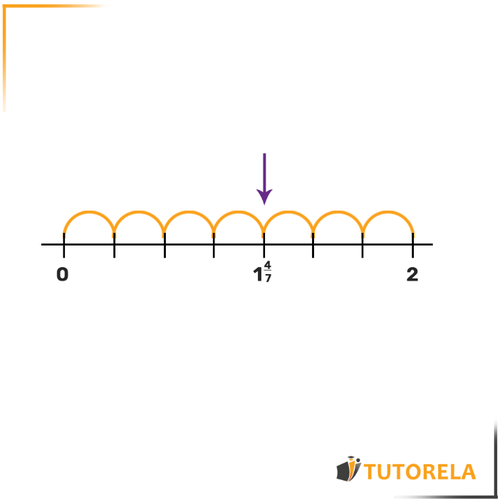
Find the number that the arrow points to:
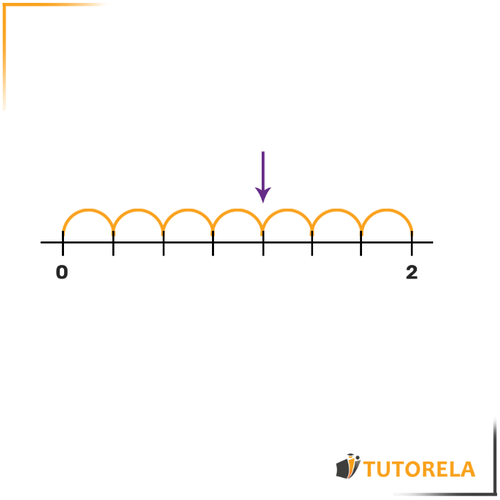
Solution:
First, let’s find out how much each segment represents.
Take the two given numbers and
and count how many segments there are between them.
There are segments between and .
Subtract:
Now divide by
Each segment represents .
Now, let's see how many segments we need to jump to reach the arrow:
The answer is , so the number will be .
Make sure not to forget the whole number .
`
`
What number is marked on the number axis?
What number is marked with a question mark (?) on the number line below?
What is the missing numebr (?) marked on the number line below?
Examples with solutions for Fractions on a Number Line
Exercise #1
What are the missing numbers (?) on the numer line below?
Video Solution
Step-by-Step Solution
Let's first count how many points, including the number 1, are on the number line.
Since there are 7 in total, we'll define the 0 point as the fraction:
We will also define 1 as the following fraction:
Now let's fill in each point on the line to discover which numbers are missing:
Answer
Exercise #2
What number is missing (?) from the number line?
Video Solution
Step-by-Step Solution
Let's first count how many points, including the number 1, there are on the number line.
Since there are 6 in total, we will define the 0 point as the fraction:
We will also define 1 as the following fraction:
Now let's fill in each point on the sequence and discover which numbers are missing:
Answer
Exercise #3
What number is missing (?) on the number line below?
Video Solution
Step-by-Step Solution
Let's first count how many points, including the number 1, there are on the number line.
Since there are 4 in total, we'll define the 0 point as the following fraction:
We can also define 1 as follows:
Finally, we can fill in each point on the number line to work out which number is represented by the question mark:
Answer
Exercise #4
What number is missing (?) from the number line below?
Video Solution
Step-by-Step Solution
Let's first count how many points, including the number 1, thre are on the number line.
Since there are 4 in total, we'll define the 0 point as the followifraction:
We will also define 1 as the following fraction:
Now let's fill in each point on the number line to discover which number is represented by the question mark:
Answer
Exercise #5
What is the missing number (?) on the number line below?
Video Solution
Step-by-Step Solution
Let's first count how many points, including the number 1, there are on the number line.
Since there are 11 in total, we'll define the 0 point as the following fraction:
We will also define 1 as the following fraction:
Now let's fill in each point on the sequence to discover what our missing number is:
Answer
More Questions
Fractions on a Number Line
- The Order of Basic Operations: Addition, Subtraction, and Multiplication
- Order of Operations: Exponents
- Order of Operations: Roots
- Division and Fraction Bars (Vinculum)
- The Numbers 0 and 1 in Operations
- Neutral Element (Identity Element)
- Order of Operations with Parentheses
- Order or Hierarchy of Operations with Fractions
- Opposite numbers
- Elimination of Parentheses in Real Numbers
- Addition and Subtraction of Real Numbers
- Multiplication and Division of Real Numbers
- Multiplicative Inverse
- Integer powering
- Positive and negative numbers and zero
- Real line or Numerical line
- Fractions
- A fraction as a divisor
- How do you simplify fractions?
- Simplification and Expansion of Simple Fractions
- Common denominator
- Hundredths and Thousandths
- Part of a quantity
- Sum of Fractions
- Subtraction of Fractions
- Multiplication of Fractions
- Division of Fractions
- Comparing Fractions
- Numerator
- Denominator
- Decimal Fractions
- What is a Decimal Number?
- Reducing and Expanding Decimal Numbers
- Addition and Subtraction of Decimal Numbers
- Comparison of Decimal Numbers
- Converting Decimals to Fractions
- Remainder of a fraction
- Decimal fraction remainder
- Remainders
- Order of Operations - Exponents and Roots
- Special cases (0 and 1, reciprocals, fraction line)









