Various Forms of the Quadratic Function

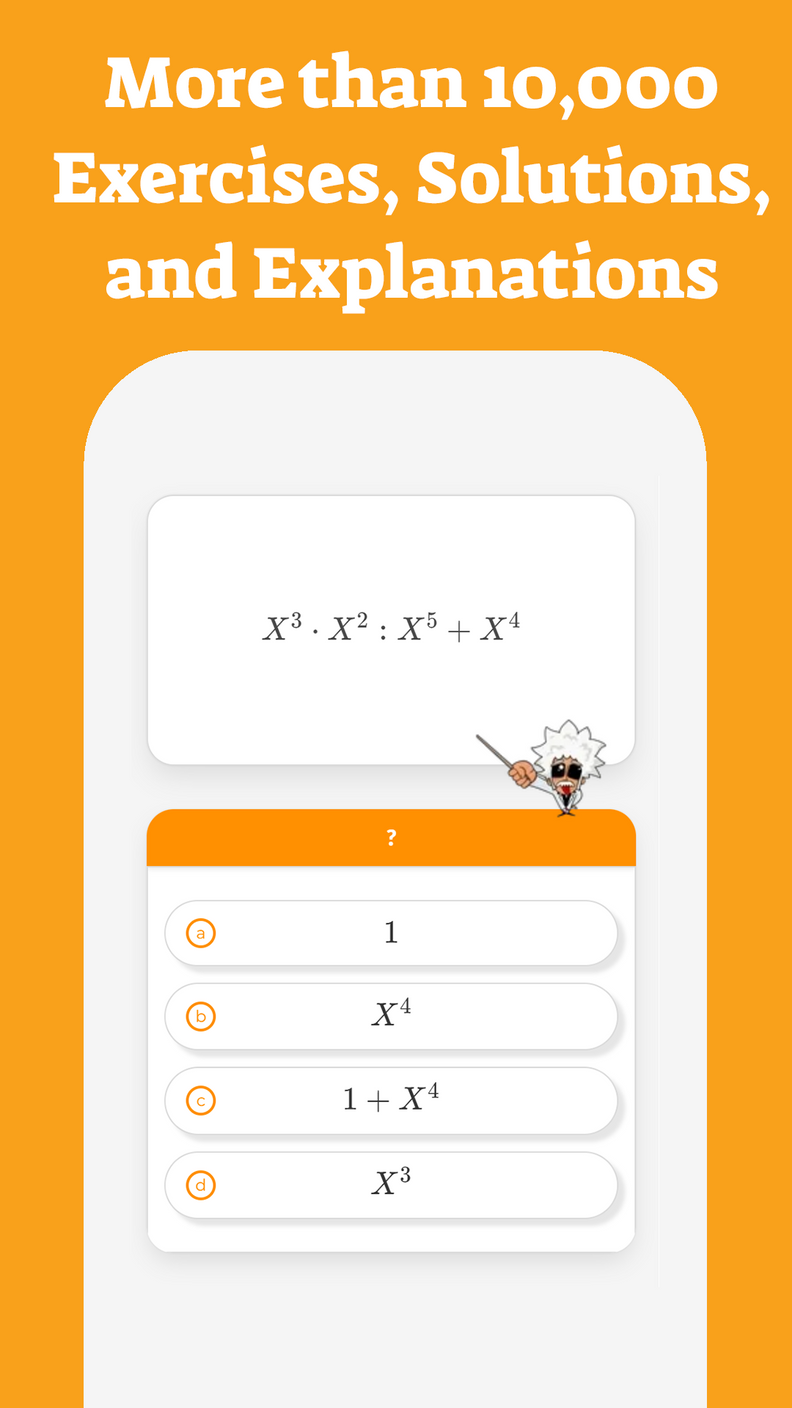
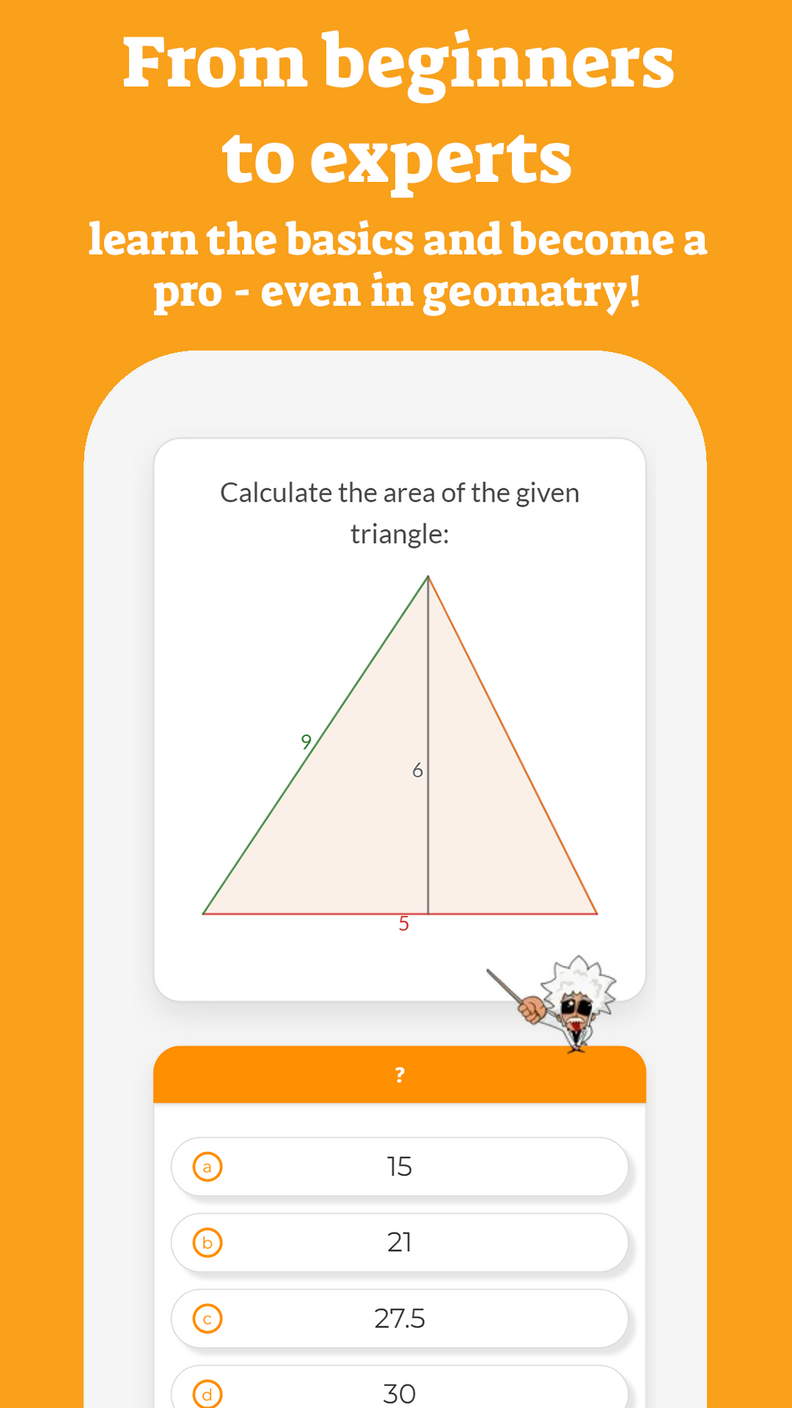
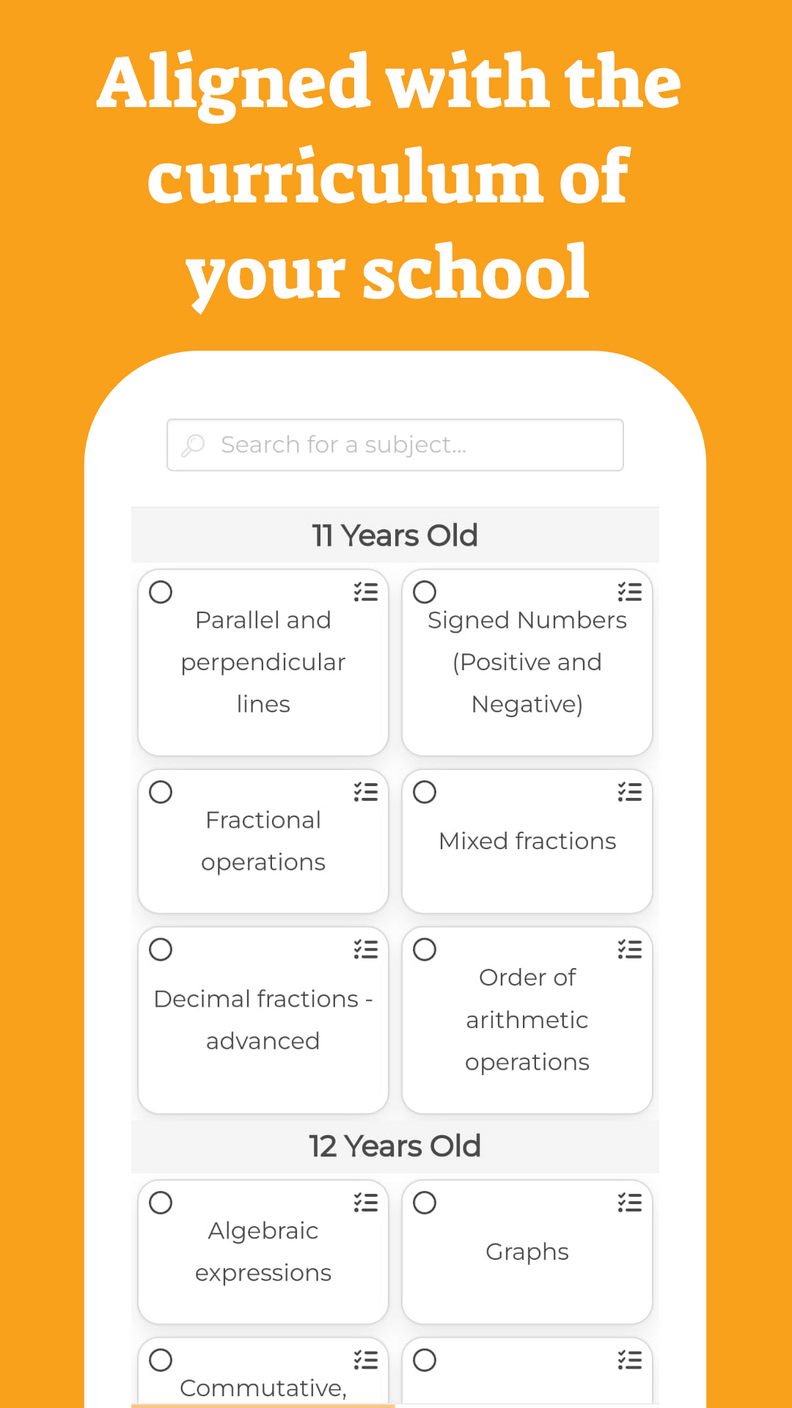
Incomplete quadratic equations are quadratic equations in which $c$,$b$ are equal to $0$.

We can solve them very easily with the following techniques and, in this way, we will avoid using the quadratic formula.

When we have an incomplete quadratic equation in which $b=0$:

We will compare between the independent term and the term with $x^2$
and will solve for $X$. We will notice that the square root has two solutions (subtraction and addition).

When we have an incomplete quadratic equation in which $c=0$ :

We will take out the common factor and find the terms that set the equation to zero.

Quadratic equations with fractional denominators

In certain cases, we will see quadratic equations as an expression with a fraction. To solve quadratic equations that include denominators, we will have to find the common denominator, multiply all the terms and thus arrive at an equation without fractions. Then we will solve it normally and find the solutions.