Repeating Decimal

In this article, we will introduce you to the repeating decimal and even teach you how to get there without needing to use a calculator. Are we ready?

To understand what a repeating decimal looks like, we must know the meaning of the word "repeating".
Something repeating is something that repeats and reappears continuously, periodically.
Even a TikTok video that repeats over and over again does so periodically.
Generally, repeating decimals are also infinite, they do not end and their numbers repeat over and over again...
Example of a repeating decimal $0.4545454545..........$
Notice that the digits $4$ and $5$ repeat continuously.

Every fraction whose denominator we cannot change to the power of $10$ – $100$, $1000$, $10000$ etc. by amplification.

First step: We will write the fraction as we write a division horizontally.

Second step: We will add the decimal point to the dividend and then several zeros, about $5$ (the value of the number will change)
Third step: We will solve the division and copy the decimal point to the result exactly in the same place it was.
Fourth step: We will write ellipses at the result to signal that the number continues.

Convert the fraction $2 \over 9$ to a repeating decimal

Solution:
We will proceed step by step:
First, we will write the exercise as a division problem.

In the second step, we will add a decimal point and some zeros to the dividend.

In the third step, we will solve the exercise according to the division rules throughout and remember to copy the decimal point to the result.

Notice what we have obtained - remainder $2$ that repeats successively
The result obtained is, without a doubt, a repeating decimal.
(Let's add ellipses after the last digit to represent continuity)

Convert the fraction $2 \over 11$ to a repeating decimal

Solution:
First, let's write the exercise as a long division and do not forget to add the decimal point and then the zeros to the dividend.

Great. Now let's solve the exercise according to the division rules and do not overlook copying the decimal point to the result.

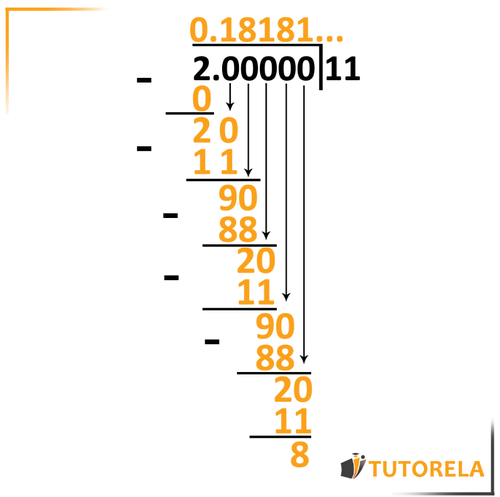
Notice what we obtained: a decimal whose digits $1$ and $8$ repeat successively in a periodic manner, that is, a repeating decimal number.

It may be that in the exam they do not mention that the fraction is, in fact,
a repeating decimal and that they simply ask you to convert it to a decimal number.
Also in this case the way to solve it and the solution will be the same.