Square Root Rules

What is a root?

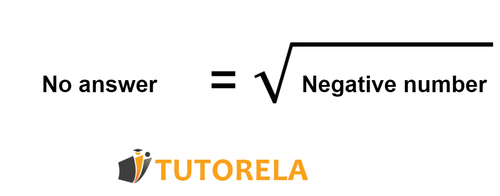
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the principal square root of $25$ is $5$ , because $5 \times 5=25$ .
The square root symbol is written as $\sqrt{\phantom{X}}$ .
for example: $\sqrt{9}=3$

Note that we typically work with non-negative numbers when finding square roots in the real number system.

Square root is basically the inverse operation of a power. Even so, it can be written as a power! Square root is equal to a power of $\sqrt{x}=x^{\frac{1}{2}}$ .

If a small number appears to the left of the square root symbol, it indicates the order of the root, also known as the index. For example, in $\sqrt[3]{8}$ , the small number $3$ tells us it is a cube root, meaning we are looking for a number that, when multiplied by itself three times, equals $8$ . When no number is shown, it is understood to be a square root (index of $2$ ).

What is necessary to know about a root?

Perfect Squares:

These are numbers whose square roots are whole numbers, like $1,4,9,16,25$ etc. For example: $\sqrt{16}=4$ because $4×4=16$ .

Non-Perfect Squares:

These are numbers that do not have a whole number square root. For instance, $\sqrt{2}$ is approximately $1.414$ , and it’s an irrational number.

Negative Numbers:

The square root of a negative number is not defined in the set of real numbers. That means the result of the square root will always be positive! You will never get a negative result. We can get a result of $0$ . For $\sqrt{}$ of a negative-number there is no answer! However, in advanced math, we use imaginary numbers (e.g., $\sqrt{-1} = i$ ) to handle these cases.

Square as a Power:

The square root is basically a half power. We can say that: $\sqrt{a}=a^{\frac{1}{2}}$

Roots in order of operations:

Square roots are evaluated along with other exponents in the standard order of operations (PEMDAS/BODMAS), after parentheses and before multiplication and division. When there are both powers and roots, we solve then from the left to the right, since they are on the same level.

Simplifying Square Roots:

When the number inside the square root has a factor that is a perfect square, you can simplify it. For example: $\sqrt{50}=\sqrt{25×2}=\sqrt{25}×\sqrt{2}=5\sqrt2$ .

The result of the square root will always be positive

Detailed explanation

Start practice

Test yourself on rules of roots!

Choose the largest value

Practice more now

What is a square root anyway?

A root is symbolized with the sign $√$
Indeed, when we see a number with a root, we wonder what positive number raised to $2$ , will give us what is written inside the root.
A root is the opposite of a power operation. When there is no small number at the top left of the root, it denotes that it is a root of $2$ , square root.
If a small number appears on the left, this will be the order of the root.

Let's know some of the definitions and properties:

The result of a root will always be positive! A negative result will never be obtained. We can get a result of $0$ .
For $√$ (negative number) there is no answer!
The root is basically a half power. We can say that: $\sqrt a=a^{ 1 \over 2}$
In the order of Operations, square roots are evaluated along with other exponents in the standard order of operations (PEMDAS/BODMAS), after parentheses and before multiplication and division.

Let's see the example:
$\sqrt {64} =8$

Let's ask, w What number times itself will give us $64$ and the answer is $8$ .
True, also $-8$ to the power of $2$ will give us $64$ but the result of the root must be positive!

Laws of Radicals

The following laws allow you to manipulate and simplify radical expressions. These rules are based on the properties of exponents and are essential for solving complex radical problems.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Solve the following exercise:

$\sqrt{\frac{2}{4}}=$

Question 2

Solve the following exercise:

$\sqrt{30}\cdot\sqrt{1}=$

Question 3

Solve the following exercise:

$\sqrt{1}\cdot\sqrt{25}=$

The root of a product

When the root appears across the entire product, we can break down each factor and apply the root to them, leaving the multiplication sign between the factors.
We formulate:
$\sqrt{(a\cdot b)}=\sqrt{a}\cdot\sqrt{b}$ [object Object]
Where $a \geq 0$ and $b \geq 0$

Let's see this in an example:
$\sqrt{(64\cdot100)}$
According to the root of a product rule, we can break down the factors and leave the root of each factor separately while maintaining the multiplication operation between them:
We will break it down and obtain:
$\sqrt{64}\cdot\sqrt{100}=$
$8\cdot10=80$

More Examples:

$\sqrt{4 \cdot 9} = \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6$
$\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}$
$\sqrt{3} \cdot \sqrt{12} = \sqrt{3 \cdot 12} = \sqrt{36} = 6$

Key Application: Use this rule to simplify radicals by factoring out perfect squares.

Square Root of a Quotient

When the root appears over the entire quotient (over the entire fraction), we can break down each factor and apply the root to it, leaving the division sign (fraction line) between the factors.
We formulate:
$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$ [object Object]
where $a \geq 0$ and $b > 0$

Let's see this in an example:

$\sqrt{\frac{36}{9}}$

According to the rule of the root of a quotient, we can break down the factors and leave the root of each factor separately while maintaining the multiplication operation between them:
We will break it down and obtain:

$\frac{\sqrt{36}}{\sqrt{9}}$

$\frac{6}{3}=2$

More Examples:

$\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2}$
$\sqrt{\frac{18}{2}} = \frac{\sqrt{18}}{\sqrt{2}} = \frac{3\sqrt{2}}{\sqrt{2}} = 3$
$\frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}} = \sqrt{25} = 5$

Important Note: This rule is commonly used for rationalizing denominators and simplifying complex fractions.

Do you know what the answer is?

Question 1

Solve the following exercise:

$\sqrt{16}\cdot\sqrt{1}=$

Question 2

Solve the following exercise:

$\sqrt{1}\cdot\sqrt{2}=$

Question 3

Solve the following exercise:

$\sqrt{25x^4}=$

Root of a Radical

When we encounter an exercise where there is a root over a root, we will multiply the order of the first root by the order of the second root and the order we obtain we will multiply as a root over our number. (As the rule of power over another power)
Let's put it this way:
$\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}$ [object Object]
Where $a \geq 0$ .

Let's see this in the example:
$\sqrt[2]{\sqrt[4]{100}}=\sqrt[2\cdot4]{100}=\sqrt[8]{100}$

More Examples:

$\sqrt{\sqrt{16}} = \sqrt[4]{16} = 2$ (since $2^4 = 16$ )
$\sqrt{\sqrt[3]{8}} = \sqrt[6]{8} = 8^{1/6}$
$\sqrt{\sqrt{x^8}} = \sqrt[4]{x^8} = x^2$ (when $x \geq 0$ )

Simplifying Complex Expressions

When working with multiple radicals, apply the rules systematically:

Step-by-Step Process:

Look for perfect square factors
Apply product/quotient rules
Combine like radicals
Rationalize denominators if needed

Examples:

Example 1: $\sqrt{72} + \sqrt{18}$

$\sqrt{72} = \sqrt{36 \cdot 2} = 6\sqrt{2}$
$\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}$
Result: $6\sqrt{2} + 3\sqrt{2} = 9\sqrt{2}$

Example 2: $\frac{\sqrt{45}}{\sqrt{5}}$

Method 1: $\frac{\sqrt{45}}{\sqrt{5}} = \sqrt{\frac{45}{5}} = \sqrt{9} = 3$
Method 2: $\sqrt{45} = \sqrt{9 \cdot 5} = 3\sqrt{5}$ , so $\frac{3\sqrt{5}}{\sqrt{5}} = 3$

Check your understanding

Question 1

Solve the following exercise:

$\sqrt{10}\cdot\sqrt{3}=$

Question 2

Solve the following exercise:

$\sqrt{7}\cdot\sqrt{7}=$

Question 3

Solve the following exercise:

$\sqrt{100}\cdot\sqrt{25}=$

Common Mistakes to Avoid

Mistake 1: $\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}$

Wrong: $\sqrt{9 + 16} = \sqrt{9} + \sqrt{16} = 3 + 4 = 7$
Correct: $\sqrt{9 + 16} = \sqrt{25} = 5$

Mistake 2: Forgetting absolute values with variables

Wrong: $\sqrt{x^2} = x$
Correct: $\sqrt{x^2} = |x|$

Mistake 3: Incorrect application of quotient rule

Wrong: $\sqrt{\frac{a}{b}} = \frac{a}{\sqrt{b}}$
Correct: $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$

Mistake 4: Forgetting domain restrictions

Remember: $\sqrt{a}$ is only defined for $a \geq 0$ in real numbers

If you are interested in this article, you may also be interested in the following articles:

The root of a product

Root of the quotient

Radication

Combining powers and roots

In the blog of Tutorela you will find a variety of articles on mathematics.

Examples and exercises with solutions on properties of roots

Exercise #1

Choose the largest value

Video Solution

Step-by-Step Solution

Let's begin by calculating the numerical value of each of the roots in the given options:

$\sqrt{25}=5\\ \sqrt{16}=4\\ \sqrt{9}=3\\$ We can determine that:

$5>4>3>1$ Therefore, the correct answer is option A

Answer

$\sqrt{25}$

Exercise #2

Solve the following exercise:

$\sqrt{\frac{2}{4}}=$

Video Solution

Step-by-Step Solution

Simplify the following expression:

Begin by reducing the fraction under the square root:

$\sqrt{\frac{2}{4}}= \\ \sqrt{\frac{1}{2}}=$

Apply two exponent laws:

A. Definition of root as a power:

$\sqrt[n]{a}=a^{\frac{1}{n}}$

B. The power law for powers applied to terms in parentheses:

$\big(\frac{a}{b}\big)^n=\frac{a^n}{b^n}$

Let's return to the expression that we obtained. Apply the law mentioned in A and convert the square root to a power:

$\sqrt{\frac{1}{2}}=\\ \big(\frac{1}{2}\big)^{\frac{1}{2}}=$

Next use the power law mentioned in B, apply the power separately to the numerator and denominator.

In the next step remember that raising the number 1 to any power will always result in 1.

In the fraction's denominator we'll return to the root notation, again, using the power law mentioned in A (in the opposite direction):

$\big(\frac{1}{2}\big)^{\frac{1}{2}}= \\ \frac{1^{\frac{1}{2}}}{2^{\frac{1}{2}}}=\\ \boxed{\frac{1}{\sqrt{2}}}\\$ Let's summarize the simplification of the given expression:

$\sqrt{\frac{2}{4}}= \\ \sqrt{\frac{1}{2}}= \\ \frac{1^{\frac{1}{2}}}{2^{\frac{1}{2}}}=\\ \boxed{\frac{1}{\sqrt{2}}}\\$ Therefore, the correct answer is answer D.

Answer

$\frac{1}{\sqrt{2}}$

Exercise #3

Solve the following exercise:

$\sqrt{30}\cdot\sqrt{1}=$

Video Solution

Step-by-Step Solution

Let's start with a reminder of the definition of a root as a power:

$\sqrt[n]{a}=a^{\frac{1}{n}}$

We will then use the fact that raising the number 1 to any power always yields the result 1, particularly raising it to the power of half of the square root (which we obtain by using the definition of a root as a power mentioned earlier).

In other words:

$\sqrt{30}\cdot\sqrt{1}= \\ \downarrow\\ \sqrt{30}\cdot\sqrt[2]{1}=\\ \sqrt{30}\cdot 1^{\frac{1}{2}}=\\ \sqrt{30} \cdot1=\\ \boxed{\sqrt{30}}$

Therefore, the correct answer is answer C.

Answer

$\sqrt{30}$

Exercise #4

Solve the following exercise:

$\sqrt{1}\cdot\sqrt{25}=$

Video Solution

Step-by-Step Solution

To solve the expression $\sqrt{1} \cdot \sqrt{25}$ , we will use the Product Property of Square Roots.

According to the property, we have:

$\sqrt{1} \cdot \sqrt{25} = \sqrt{1 \cdot 25}$

First, calculate the product inside the square root:

$1 \cdot 25 = 25$

Now the expression simplifies to:

$\sqrt{25}$

Finding the square root of 25 gives us:

$5$

Thus, the value of $\sqrt{1} \cdot \sqrt{25}$ is $\boxed{5}$ .

After comparing this solution with the provided choices, we see that the correct answer is choice 3.

Answer

$5$

Exercise #5

Solve the following exercise:

$\sqrt{16}\cdot\sqrt{1}=$

Video Solution

Step-by-Step Solution

Let's start by recalling how to define a root as a power:

$\sqrt[n]{a}=a^{\frac{1}{n}}$

Next, we will remember that raising 1 to any power will always yield the result 1, even the half power of the square root.

In other words:

$\sqrt{16}\cdot\sqrt{1}= \\ \downarrow\\ \sqrt{16}\cdot\sqrt[2]{1}=\\ \sqrt{16}\cdot 1^{\frac{1}{2}}=\\ \sqrt{16} \cdot1=\\ \sqrt{16} =\\ \boxed{4}$ Therefore, the correct answer is answer D.

Answer

$4$

Do you think you will be able to solve it?

Question 1

Solve the following exercise:

$\sqrt{25}\cdot\sqrt{4}=$

Question 2

Solve the following exercise:

$\sqrt{9}\cdot\sqrt{4}=$

Question 3

Solve the following exercise:

$\sqrt{100x^2}=$

Start practice

Square Root Rules

What is a root?

What is necessary to know about a root?

Perfect Squares:

Non-Perfect Squares:

Negative Numbers:

Square as a Power:

Roots in order of operations:

Simplifying Square Roots:

Test yourself on rules of roots!

What is a square root anyway?

Laws of Radicals

The root of a product

Square Root of a Quotient

Root of a Radical

Simplifying Complex Expressions

Common Mistakes to Avoid

Examples and exercises with solutions on properties of roots

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

More Questions

Rules of Roots Combined