The Parabola
This function is a quadratic function and is called a parabola.
We will focus on two main types of parabolas: maximum and minimum parabolas.
This function is a quadratic function and is called a parabola.
We will focus on two main types of parabolas: maximum and minimum parabolas.
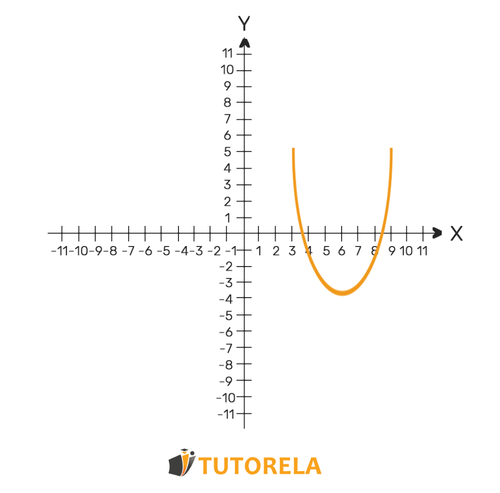
Also called smiling or happy.
A vertex is the minimum point of the function, where is the lowest.
We can identify that it is a minimum parabola if the equation is positive.
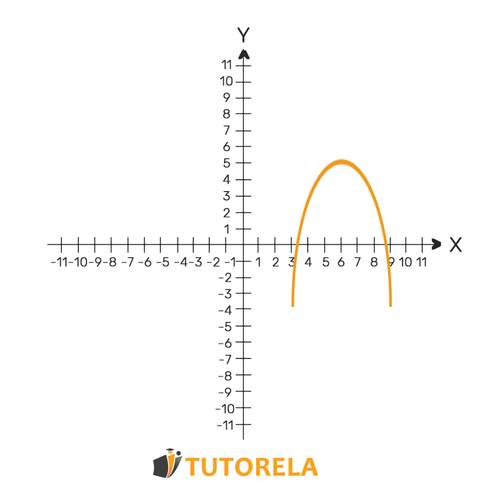
Also called sad or crying.
A vertex is the maximum point of the function, where is the highest.
We can identify that it is a maximum parabola if the equation is negative.
To the parabola,
the vertex marks its highest point.
How do we find it?
Determine the value of the coefficient \( a \) in the following equation:
\( -x^2+7x-9 \)
One of the following two methods can be chosen:
The value of that we receive will be replaced in the parabola function and we will obtain the value of relevant.
What is the value of the coefficient \( b \) in the equation below?
\( 3x^2+8x-5 \)
What is the value of the coefficient \( c \) in the equation below?
\( 4x^2+9x-2 \)
What is the value of the coefficient \( c \) in the equation below?
\( 3x^2+5x \)
The formula to find a vertex using two symmetric points is:
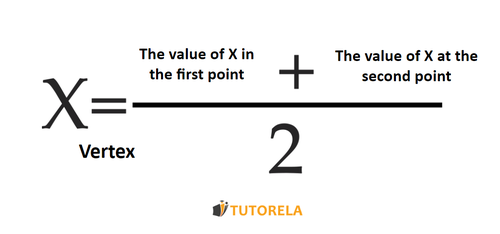
The vertex that we receive in the function to find the value of the vertex .
Now, we will move on to the points of intersection of the parabola with the and axes
When we want to find the point of intersection with the axis:
We will set in the quadratic equation and solve using a trinomial or the root formula.
We can find parabolas that are not zero and that do not have any point of intersection with the axis, or that have or a maximum of .
When we want to find a point of intersection with the axis:
We will set in the quadratic equation and find the solutions.
Wonderful. Now we will move on to the areas of increase and decrease of the quadratic function.
Identify the coefficients based on the following equation
\( y=x^2+x+5 \)
Identify the coefficients based on the following equation
\( y=-x^2+x+5 \)
Identify the coefficients based on the following equation
\( y=3x^2+3x-4 \)
The areas of increase and decrease describe the where the parabola increases and where the parabola decreases.
The parabola changes its domain once, at the vertex.
Let's see this in the figure:

When there is a graph:
We will examine what happens when the s are smaller than the vertex and what happens when the s are greater than the vertex .
When there is no graph:
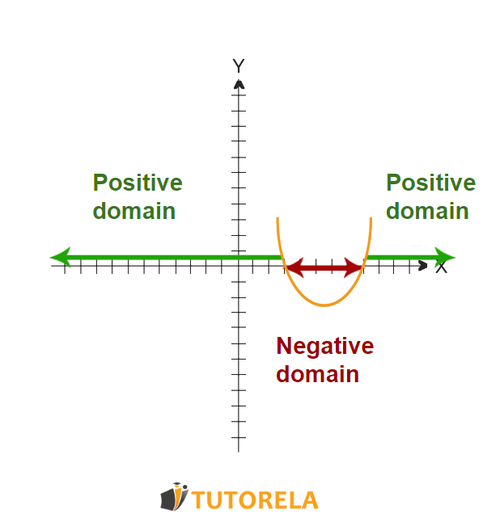
Positive domain: describes the where the graph of the parabola is above the axis, with a value positive.
Negative domain: describes the where the graph of the parabola is below the axis, with a negative value.
To find the domains of positivity and negativity, we will plot the graph of the parabola and ask:
At what values is the graph of the parabola above the axis, with a positive value? This will be the domain of positivity of the parabola.
At what values is the graph of the parabola below the axis, with a negative value? This will be the domain of negativity of the parabola.
Let's see this on the graph:
Determine the value of the coefficient in the following equation:
The quadratic equation in the problem is already arranged (meaning all terms are on one side and 0 on the other side), so let's proceed to answer the question asked:
The question asked in the problem - What is the value of the coefficient in the equation?
Let's recall the definitions of coefficients in solving quadratic equations and the roots formula:
The rule states that the roots of an equation of the form:
are:
That is the coefficient is the coefficient of the quadratic term (meaning the term with the second power)- Let's examine the equation in the problem:
Remember that the minus sign before the quadratic term means multiplication by: , therefore- we can write the equation as:
The number that multiplies the , is hence we identify that the coefficient of the quadratic term is the number ,
Therefore the correct answer is A.
-1
What is the value of the coefficient in the equation below?
The quadratic equation of the given problem is already arranged (that is, all the terms are found on one side and the 0 on the other side), thus we approach the given problem as follows;
In the problem, the question was asked: what is the value of the coefficientin the equation?
Let's remember the definitions of coefficients when solving a quadratic equation as well as the formula for the roots:
The rule says that the roots of an equation of the form
are :
That is the coefficientis the coefficient of the term in the first power -We then examine the equation of the given problem:
That is, the number that multiplies
is
Consequently we are able to identify b, which is the coefficient of the term in the first power, as the number,
Thus the correct answer is option d.
8
What is the value of the coefficient in the equation below?
The quadratic equation is given as . This equation is in the standard form of a quadratic equation, which is , where , , and are coefficients.
From this analysis, we can see that the coefficient is .
Therefore, the value of the coefficient in the equation is .
-2
What is the value of the coefficient in the equation below?
The quadratic equation of the given problem has already been arranged (that is, all the terms are on one side and 0 is on the other side) thus we can approach the question as follows:
In the problem, the question was asked: what is the value of the coefficientin the equation?
Let's remember the definition of a coefficient when solving a quadratic equation as well as the formula for the roots:
The rule says that the roots of an equation of the form
are:
That is the coefficient
is the free term - and as such the coefficient of the term is raised to the power of zero -(Any number other than zero raised to the power of zero equals 1:
)
Next we examine the equation of the given problem:
Note that there is no free term in the equation, that is, the numerical value of the free term is 0, in fact the equation can be written as follows:
and therefore the value of the coefficient is 0.
Hence the correct answer is option c.
0
Identify the coefficients based on the following equation
To solve this problem, we will identify the parameters of the given quadratic function step-by-step:
Now, let's analyze the quadratic function provided:
From the given expression :
- The coefficient of is , so .
- The coefficient of is , so .
- The constant term is , so .
Therefore, the parameters of the quadratic function are , , and .
Consequently, the correct choice from the provided options is .
Identify the coefficients based on the following equation
\( y=-4x^2+3 \)
Identify the coefficients based on the following equation
\( y=-3x^2-4 \)
Identify the coefficients based on the following equation
\( y=-5x^2 \)