Area of a Scalene Triangle

It's very simple to calculate the area of a scalene triangle if we remember the formula and strictly follow the steps. Don't worry, we're here to teach you exactly what to pay attention to—we won't leave you adrift!
First of all, let's look at the formula you need to remember in order to calculate the area of the scalene triangle:

Multiply the height by the base (the side corresponding to that height) and divide by $2$.

Pay attention:

Make sure to place in the formula the corresponding height and side. That is, if a certain height and a side that does not form a right angle of $90^o$ degrees with the used height is placed in the formula, it will be wrong.

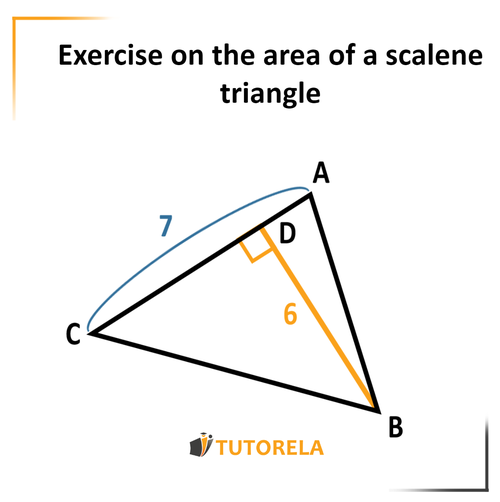
Given the triangle $ABC$
Given that:
$DB=6$ Height
$AC = 7$
What is the area of the triangle?

Solution:
We will see that the given side $AC$ actually forms, with the height, an angle of $90^o$ degrees.
After verifying the data, we will go to the formula and place there:
$\frac{6\times7}{2}=21$

The area of the triangle $ABC$ is $21\operatorname{cm}^2$

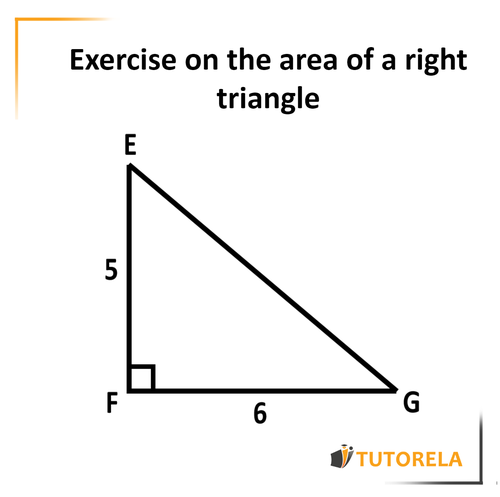
Given the right triangle $EFG$
Given that:
angle $EFG = 90$
$EF=5$
$FG=6$
Calculate the area of the triangle.

Solution:
Let's remember that the key to calculating the area of any triangle is to multiply the height
by the corresponding side and then divide that product by$2$
In a right triangle, we actually already have the height!
We don't need to calculate another height and, in fact, we can afford to use the given height along with the side that forms the $90^o$ degree angle.

In our exercise: The side is $EF$ or $FG$

What conclusion do we reach?
The conclusion is that the formula to calculate the area of a right triangle is the product of the two legs divided by $2$Let's put it in the formula and we will get:

$\frac{6\times5}{2}=15$
The area of the triangle $EFG$ is $15cm^2$

Calculating the area of an obtuse triangle is a bit more complicated, but I assure you that once you understand the basic principle, you will be able to calculate the area of an obtuse triangle even in your sleep...
In certain cases, in an obtuse triangle, we will be given a height that is outside the triangle.
As in the following illustration:

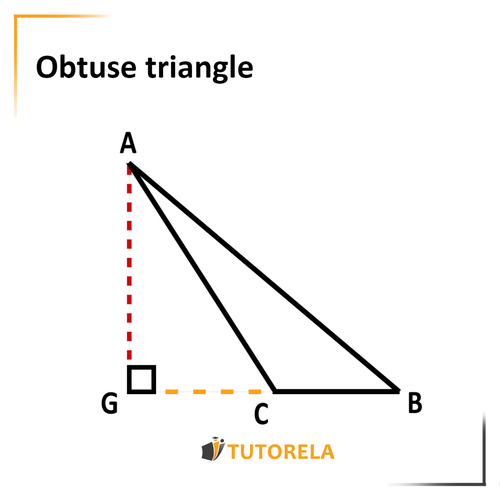
In this illustration, the height $AG$ has been drawn outside of the triangle. In reality, if we were to extend the side $CB$ (marked in green), it would form a right angle with the height.
How is the area of an obtuse triangle calculated?

Remember the following guidelines and you will do well:

• In calculating the area of the obtuse triangle, we refer to the actual side length of the triangle and not to its dotted extension.
• In calculating the area of the obtuse triangle, we refer to the given height (even if it is outside the triangle) and look for the corresponding side, which together with it forms a $90^o$ degree angle when extended outside the triangle.

Now let's solve an exercise so you can understand it more easily:

Given the triangle $\triangle ABC$
Given that:
$BD= 2$ Height of the triangle
$AD= 5$
$CD= 12$

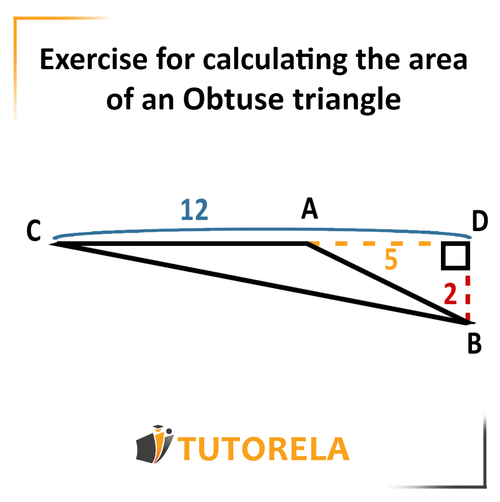
What is the area of the triangle?

Solution:
We observe that the length of the side $DB = 2$
and the corresponding side that forms with it a $90^o$ degree angle (the dotted part outside the triangle) is $CA$
If we go back to the first point we needed to remember - we will understand that, to calculate the area, we must only take into account the length of $AC$ without its dotted extension.
Therefore, we will see it as $12-5=7$
$AC=7$
And now we can safely place the data, according to the basic formula:
$\frac{7\times2}{2}=7$
The area of the triangle $ABC$ is $7cm^2$