Isosceles Triangle Practice Problems and Exercises

Master isosceles triangles with step-by-step practice problems. Learn to identify equal sides, calculate base angles, and solve vertex angle problems.

📚Master Isosceles Triangle Properties Through Practice
  • Identify equal sides and legs in isosceles triangles
  • Calculate base angles using the equal angles property
  • Find vertex angles when given base angle measurements
  • Classify isosceles triangles as acute, right, or obtuse
  • Apply the angle sum property to solve triangle problems
  • Distinguish between base angles and vertex angles in examples

Understanding Isosceles triangle

Complete explanation with examples

Definition of isosceles triangle

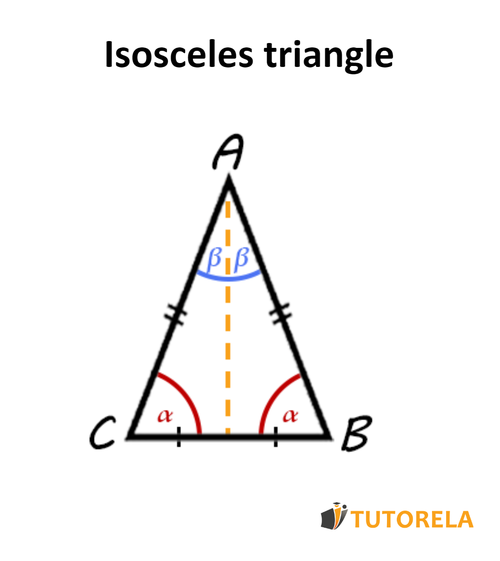
The isosceles triangle is a type of triangle that has two sides (legs) of equal length.

A consequence of having two sides of equal length implies that also the two angles opposite these sides measure the same.

Key Parts:

  • Legs: The two equal sides
  • Base: The third side (different length)
  • Vertex angle: The angle between the two legs
  • Base angles: The two equal angles adjacent to the base

This fundamental property—that equal sides create equal opposite angles—makes isosceles triangles essential building blocks in geometry and forms the basis for the Isosceles Triangle Theorem.

A - Identification of an isosceles triangle

Detailed explanation

Practice Isosceles triangle

Test your knowledge with 20 quizzes

Is the triangle in the drawing a right triangle?

Examples with solutions for Isosceles triangle

Step-by-step solutions included
Exercise #1

Is the triangle in the drawing an acute-angled triangle?

Step-by-Step Solution

An acute-angled triangle is defined as a triangle where all three interior angles are less than 90∘90^\circ.

In examining the visual depiction of the triangle provided in the problem, we need to see if it appears to satisfy this property. The assessment relies on observing the triangle's structure shown in the drawing and noting any geometric indications suggesting angle types.

Given the information from the drawing, if all angles seem to satisfy the condition of being less than 90∘90^\circ, then by definition, the triangle is an acute-angled triangle.

Conclusively, the answer to whether the triangle is acute-angled based on provided visual assessment and inherent assumptions in its illustration is: Yes.

Answer:

Yes

Video Solution
Exercise #2

In an isosceles triangle, the angle between ? and ? is the "base angle".

Step-by-Step Solution

An isosceles triangle is one that has at least two sides of equal length. The angles opposite these two sides are known as the "base angles."
The side that is not equal to the other two is referred to as the "base" of the triangle. Thus, the "base angles" are the angles between each of the sides that are equal in length and the base.
Therefore, when we specify the angle in terms of its location or position, it is the angle between a "side" and the "base." This leads to the conclusion that the angle between the side and the base is the "base angle."

Therefore, the correct choice is Side, base.

Answer:

Side, base.

Exercise #3

What kind of triangle is given in the drawing?

404040707070707070AAABBBCCC

Step-by-Step Solution

As all the angles of a triangle are less than 90° and the sum of the angles of a triangle equals 180°:

70+70+40=180 70+70+40=180

The triangle is isosceles.

Answer:

Isosceles triangle

Video Solution
Exercise #4

Given the values of the sides of a triangle, is it a triangle with different sides?

9.19.19.19.59.59.5AAABBBCCC9

Step-by-Step Solution

As is known, a scalene triangle is a triangle in which each side has a different length.

According to the given information, this is indeed a triangle where each side has a different length.

Answer:

Yes

Video Solution
Exercise #5

Which kind of triangle is given in the drawing?

666666666AAABBBCCC

Step-by-Step Solution

As we know that sides AB, BC, and CA are all equal to 6,

All are equal to each other and, therefore, the triangle is equilateral.

Answer:

Equilateral triangle

Video Solution

Frequently Asked Questions

Everything you need to know about Isosceles triangle

How do you identify an isosceles triangle?

+
An isosceles triangle has two sides of equal length called legs. You can identify it by looking for two equal sides or two equal angles opposite those sides.

What are base angles in an isosceles triangle?

+
Base angles are the two angles adjacent to the base (the unequal side) of an isosceles triangle. These angles are always equal to each other and are always acute angles (less than 90°).

How do you find the vertex angle of an isosceles triangle?

+
To find the vertex angle: 1) Add the two base angles together, 2) Subtract this sum from 180°, 3) The result is your vertex angle. Remember that all triangle angles sum to 180°.

Can an isosceles triangle have a right angle?

+
Yes, an isosceles triangle can have a right angle (90°) at the vertex. In this case, the two base angles would each measure 45°, since 180° - 90° = 90°, and 90° ÷ 2 = 45°.

What is the difference between legs and base in isosceles triangles?

+
The legs are the two equal sides of an isosceles triangle, while the base is the third side that has a different length. The vertex angle lies between the two legs.

How do you solve isosceles triangle angle problems?

+
Use these key properties: 1) Base angles are equal, 2) All angles sum to 180°, 3) If you know one base angle, the other base angle is the same, 4) Subtract the sum of base angles from 180° to find the vertex angle.

Can base angles in an isosceles triangle be obtuse?

+
No, base angles in an isosceles triangle cannot be obtuse (greater than 90°). If they were obtuse, their sum would exceed 180°, which is impossible since all three angles must sum to exactly 180°.

What are the types of isosceles triangles?

+
Isosceles triangles are classified by their vertex angle: 1) Acute isosceles - vertex angle less than 90°, 2) Right isosceles - vertex angle equals 90°, 3) Obtuse isosceles - vertex angle greater than 90°.

More Isosceles triangle Questions

Click on any question to see the complete solution with step-by-step explanations

Types of Triangles

Parallel Line Geometry: Classifying Triangle ABC with Extended Side AE Right Triangle Area Problem: Solve for X When Area = 6 cm² Triangle Classification: Identifying a Right Triangle with 90-Degree Angle Square Diagonal Properties: Classifying Triangles ABC and ACD Isosceles Triangle ABC with Parallel Line ED: Investigating Triangle Properties

Continue Your Math Journey

Master Isosceles triangle first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

AreaThe sides or edges of a triangleTriangle HeightThe Sum of the Interior Angles of a TriangleExterior angles of a triangleTypes of TrianglesObtuse TriangleEquilateral triangleIdentification of an Isosceles TriangleScalene triangleAcute triangleThe Area of a TriangleArea of a right triangleArea of Isosceles TrianglesArea of a Scalene TriangleArea of Equilateral TrianglesAreas of Polygons for 7th GradeRight TriangleMedian in a triangleCenter of a Triangle - The Centroid - The Intersection Point of MediansHow do we calculate the area of complex shapes?How to calculate the area of a triangle using trigonometry?All terms in triangle calculationPerimeterTrianglePerimeter of a triangleHow do we calculate the perimeter of polygons?

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Applying the formula Calculate The Missing Side based on the formula Finding the size of angles in a triangle Identifying and defining elements Solving an equation by multiplying/dividing both sides Using Pythagoras' theorem Using variables