Throughout geometry studies, which deal with various structures and shapes, you are required to calculate areas and perimeters. Each shape or structure has a different formula through which you can answer the question and calculate the area. Fortunately, there is one formula that can be applied to all triangles, and it can be used to calculate the area of a triangle using trigonometry.
Triangle Area Using Trigonometry Practice Problems
Master calculating triangle area with trigonometry formulas through step-by-step practice problems. Perfect for geometry students learning sin, cos, tan applications.
- Apply the formula Area = (1/2)ab sin(C) to find triangle areas
- Calculate areas using two sides and included angle measurements
- Work with degrees and radians in trigonometric area calculations
- Solve real-world problems involving triangle area using trigonometry
- Practice with right triangles, isosceles triangles, and scalene triangles
- Convert between different angle measurements for accurate calculations
Understanding Area of a Triangle
How to calculate the area of a triangle using trigonometry?
In the field of mathematics, emphasis is also placed on trigonometry, which deals with the study of triangles, their angles, and sides. Every student is required to demonstrate knowledge of triangles (from right triangles to isosceles triangles), and thus also answer the question of how to calculate the area of a triangle using trigonometry.
One formula for all different triangles
Now that you know the formula for calculating the area of a triangle using trigonometry, you can use it in any question where you need to calculate areas in triangles. The formula for calculating the triangle:
Practice Area of a Triangle
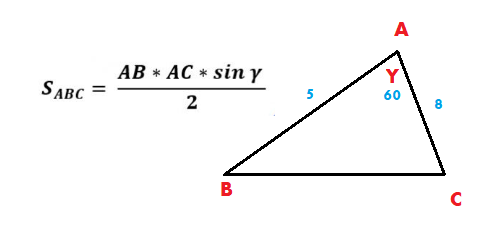
Calculate the area of the triangle using the data in the figure below.
Examples with solutions for Area of a Triangle
Calculate the area of the right triangle below:
Due to the fact that AB is perpendicular to BC and forms a 90-degree angle,
it can be argued that AB is the height of the triangle.
Hence we can calculate the area as follows:
Answer:
24 cm²
Calculate the area of the triangle ABC using the data in the figure.
First, let's remember the formula for the area of a triangle:
(the side * the height that descends to the side) /2
In the question, we have three pieces of data, but one of them is redundant!
We only have one height, the line that forms a 90-degree angle - AD,
The side to which the height descends is CB,
Therefore, we can use them in our calculation:
Answer:
36 cm²
What is the area of the triangle in the drawing?
First, we will identify the data points we need to be able to find the area of the triangle.
the formula for the area of the triangle: height*opposite side / 2
Since it is a right triangle, we know that the straight sides are actually also the heights between each other, that is, the side that measures 5 and the side that measures 7.
We multiply the legs and divide by 2
Answer:
17.5
Calculate the area of the following triangle:
The formula for calculating the area of a triangle is:
(the side * the height from the side down to the base) /2
That is:
We insert the existing data as shown below:
Answer:
10
Calculate the area of the following triangle:
The formula for the area of a triangle is
Let's insert the available data into the formula:
(7*6)/2 =
42/2 =
21
Answer:
21