Area of Isosceles Triangles - Examples, Exercises and Solutions

The triangle we are looking at is the large triangle - ABC

The triangle is formed by three sides AB, BC, and CA.

Now let's remember what we need for the calculation of a triangular area:

(side x the height that descends from the side)/2

Therefore, the first thing we must find is a suitable height and side.

We are given the side AC, but there is no descending height, so it is not useful to us.

The side AB is not given,

And so we are left with the side BC, which is given.

From the side BC descends the height AD (the two form a 90-degree angle).

It can be argued that BC is also a height, but if we delve deeper it seems that CD can be a height in the triangle ADC,

and BD is a height in the triangle ADB (both are the sides of a right triangle, therefore they are the height and the side).

As we do not know if the triangle is isosceles or not, it is also not possible to know if CD=DB, or what their ratio is, and this theory fails.

Let's remember again the formula for triangular area and replace the data we have in the formula:

(side* the height that descends from the side)/2

Now we replace the existing data in this formula:

$\frac{CB\times AD}{2}$

$\frac{11.6\times3}{2}$

$\frac{34.8}{2}=17.4$

This question is a bit confusing. We need start by identifying which parts of the data are relevant to us.

Remember the formula for the area of a triangle:

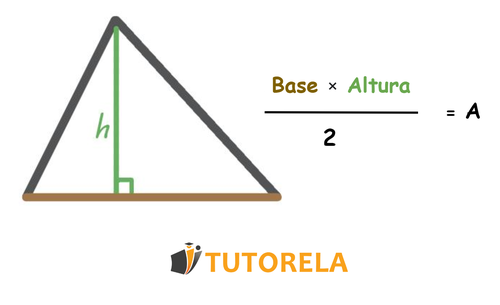The height is a straight line that comes out of an angle and forms a right angle with the opposite side.

In the drawing we have a height of 6.

It goes down to the opposite side whose length is 5.

And therefore, these are the data points that we will use.

We replace in the formula:

$\frac{6\times5}{2}=\frac{30}{2}=15$

First, we will identify the data points we need to be able to find the area of the triangle.

the formula for the area of the triangle: height*opposite side / 2

Since it is a right triangle, we know that the straight sides are actually also the heights between each other, that is, the side that measures 5 and the side that measures 7.

We multiply the legs and divide by 2

$\frac{5\times7}{2}=\frac{35}{2}=17.5$

First, let's remember the formula for the area of a triangle:

(the side * the height that descends to the side) /2

In the question, we have three pieces of data, but one of them is redundant!

We only have one height, the line that forms a 90-degree angle - AD,

The side to which the height descends is CB,

Therefore, we can use them in our calculation:

$\frac{CB\times AD}{2}$

$\frac{8\times9}{2}=\frac{72}{2}=36$

Due to the fact that AB is perpendicular to BC and forms a 90-degree angle,

it can be argued that AB is the height of the triangle.

Hence we can calculate the area as follows:

$\frac{AB\times BC}{2}=\frac{8\times6}{2}=\frac{48}{2}=24$

To determine whether it's possible to calculate the area of triangle $ABC$ with the given side $BC = 5$ cm and segment $AD = 4$ cm, we need more information than currently provided.

The possibilities for calculating the area of a triangle generally rely on knowing:

• the base and the corresponding height
• all three sides
• two sides and the included angle

In this problem, we lack sufficient data to directly apply any of these methods. Specifically:

• We do not know if $AD$ is perpendicular to $BC$, which would make it a height usable in the base-height formula.
• We only know one full side, $BC$, and a segment, $AD$, but no additional sides or angles.
• Without confirmation that $AD$ serves as an altitude or precise geometric location or measurements of angle $\angle BAC$, further calculations can't proceed.

Thus, with the given information, we cannot conclusively determine the area of triangle $ABC$.

Therefore, the solution to the problem is it is not possible.

The formula for the area of a triangle is

$A = \frac{h\cdot base}{2}$

Let's insert the available data into the formula:

(7*6)/2 =

42/2 =

21

The formula for calculating the area of a triangle is:

(the side * the height from the side down to the base) /2

That is:

$\frac{BC\times AE}{2}$

We insert the existing data as shown below:

$\frac{4\times5}{2}=\frac{20}{2}=10$

To solve this problem, we'll follow these steps:

• Step 1: Identify the given dimensions: the base $BC = 8$ units, and the height $AE = 10$ units.
• Step 2: Apply the triangle area formula: $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$.
• Step 3: Perform the calculations using the identified dimensions.

Now, let's work through each step:

Step 1: We have the base $BC = 8$ units and the height from $A$ to $BC$, which is $AE = 10$ units.

Step 2: Using the formula for the area of a triangle, we write:

Step 3: Plugging in our values, we calculate:

Therefore, the area of the triangle is 40 square units.

To find the area of the triangle, we will use the formula for the area of a triangle:

$\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$

From the problem:

• The length of the base $BC$ is given as 7 units.
• The height from point $A$ perpendicular to the base $BC$ is given as 4.5 units.

Substitute the given values into the area formula:

$\text{Area} = \frac{1}{2} \times 7 \times 4.5$

Calculate the expression step-by-step:

$\text{Area} = \frac{1}{2} \times 31.5$

$\text{Area} = 15.75$

Therefore, the area of the triangle is $15.75$ square units. This corresponds to the given choice: $15.75$.

To solve this problem, we'll follow these steps:

• Step 1: Identify the given base and height.
• Step 2: Apply the formula for the area of a triangle.
• Step 3: Perform the calculation to find the area.

Now, let's work through each step:
Step 1: The base of the triangle is $6.5$ and the height is $3$.
Step 2: We'll use the formula for the area of a triangle, given by: $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$.
Step 3: Plugging in our values, we get:

$\text{Area} = \frac{1}{2} \times 6.5 \times 3 = \frac{1}{2} \times 19.5 = 9.75$

Therefore, the area of the triangle is $\boxed{9.75}$.

To solve this problem, we'll use the formula for the area of a triangle given its base and height:

• Step 1: Identify the base and the height of the triangle from the given information.
• Step 2: Apply the triangle area formula.
• Step 3: Calculate the area using these values.

Now, let's apply these steps:

Step 1: From the given problem, we know:
- The base $BC$ of the triangle is $4$ units.
- The height $AE$, which is perpendicular to $BC$, is $8.5$ units.

Step 2: Use the formula for the area of the triangle:
$\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$

Step 3: Substitute the values into the formula:
$\text{Area} = \frac{1}{2} \times 4 \times 8.5 = 2 \times 8.5 = 17$

Hence, the area of the triangle is 17 square units.

To solve for the area of a triangle when the base and height are given, we'll use the formula:

$\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$

Given:

• Base = $4$ units

• Height = $7$ units

Apply the formula:

$\begin{aligned} \text{Area} &= \frac{1}{2} \times 4 \times 7 \\ &= \frac{1}{2} \times 28 \\ &= 14 \end{aligned}$

Thus, the area of the triangle is $14$ square units.

To find the area of the given triangle, we will follow these steps:

• Step 1: Identify the given base and height from the problem.
• Step 2: Apply the formula for the area of a triangle.
• Step 3: Calculate the area by substituting the values into the formula.

Let's work through the problem:

Step 1: The base $|AB|$ of the triangle is given as 8 units, and the height $|BC|$ is 6 units.

Step 2: The formula for the area of a triangle is:

$A = \frac{1}{2} \times \text{base} \times \text{height}$

Step 3: Substitute the given values into the formula:

$A = \frac{1}{2} \times 8 \times 6$

Perform the multiplication:

$A = \frac{1}{2} \times 48 = 24$

Therefore, the area of the triangle is $\mathbf{24}$ square units.

To solve this problem, we'll follow these steps:

• Step 1: Identify the given information
• Step 2: Apply the appropriate formula
• Step 3: Perform the necessary calculations

Now, let's work through each step:

Step 1: We are given that $AC = 9$ (the height) and $BC = 10$ (the base) of the triangle.

Step 2: We'll use the formula for the area of a triangle: $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$.

Step 3: Plugging in our values, we have:

Therefore, the area of the triangle is $45$.