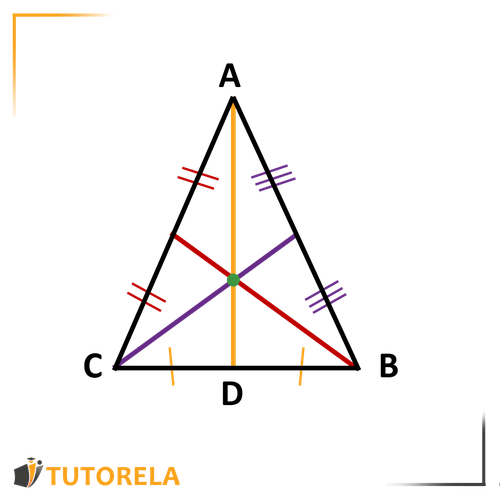
A median in a triangle is a line segment that extends from a vertex to the midpoint of the opposite side, dividing it into two equal parts.
Triangle Median Practice Problems and Worksheets
Master triangle medians with step-by-step practice problems. Learn to find medians, calculate areas, and solve centroid problems in triangles.
📚Master Triangle Medians with Interactive Practice
- Identify and draw all three medians from vertices to opposite side midpoints
- Calculate median lengths in right triangles using the hypotenuse rule
- Find areas of triangles created when medians divide the original triangle
- Solve problems involving medians in equilateral and isosceles triangles
- Locate the centroid where all three medians intersect
- Apply median properties to find missing side lengths and angles
Understanding Parts of a Triangle
Complete explanation with examples
Median in a triangle
Additional properties:
- In every triangle, it is possible to draw 3 medians.
- All 3 medians intersect at one point.
- The median to a side in a triangle creates 2 triangles of equal area.
- In an equilateral triangle - the median is also a height and an angle bisector.
- In an isosceles triangle - the median from the vertex angle is also a height and an angle bisector.
- In a right triangle - the median to the hypotenuse equals half the hypotenuse.
Practice Parts of a Triangle
Test your knowledge with 36 quizzes
Given the following triangle:
Write down the height of the triangle ABC.
Examples with solutions for Parts of a Triangle
Step-by-step solutions included
Exercise #1
True or false:
DE not a side in any of the triangles.
Step-by-Step Solution
To solve the problem of determining whether DE is not a side in any of the triangles, we will methodically identify the triangles present in the diagram and examine their sides:
- Identify triangles in the diagram. The diagram presented forms a right-angled triangle ABC with additional lines forming smaller triangles within.
- Triangles formed: Triangle ABC (major triangle), Triangle ABD, Triangle BEC, and Triangle DBE.
- Let's examine the sides of these triangles:
- Triangle ABC has sides AB, BC, and CA.
- Triangle ABD has sides AB, BD, and DA.
- Triangle BEC has sides BE, EC, and CB.
- Triangle DBE has sides DB, BE, and ED.
- Notice that while point D is used, the segment DE is only part of line BE and isn't listed as a direct side of any triangle.
Therefore, the claim that DE is not a side in any of the triangles is indeed correct.
Hence, the answer is True.
Answer:
True
Video Solution
Exercise #2
Is DE side in one of the triangles?
Step-by-Step Solution
Since line segment DE does not correspond to a full side of any of the triangles present within the given geometry, we conclude that the statement “DE is a side in one of the triangles” is Not true.
Answer:
Not true
Video Solution
Exercise #3
True or false:
AB is a side of the triangle ABC.
Step-by-Step Solution
To solve this problem, let's clarify the role of AB in the context of triangle ABC by analyzing its diagram:
- Step 1: Identify the vertices of the triangle. According to the diagram, the vertices of the triangle are points labeled A, B, and C.
- Step 2: Determine the sides of the triangle. In any triangle, the sides are the segments connecting pairs of distinct vertices.
- Step 3: Identify AB as a line segment connecting vertex A and vertex B, labeled directly in the diagram.
Considering these steps, line segment AB connects vertex A with vertex B, and hence, forms one of the sides of the triangle ABC. Therefore, AB is indeed a side of triangle ABC as shown in the diagram.
The conclusion here is solidly supported by our observation of the given triangle. Thus, the statement that AB is a side of the triangle ABC is True.
Answer:
True
Video Solution
Exercise #4
True or false:
AD is a side of triangle ABC.
Step-by-Step Solution
To determine if line segment AD is a side of triangle ABC, we need to agree on the definition of a triangle's side. A triangle consists of three sides, each connecting pairs of its vertices. In triangle ABC, these sides are AB, BC, and CA. Each side is composed of a direct line segment connecting the listed vertices.
In the diagram provided, there is no indication of a point D connected to point A or any other vertex of triangle ABC. To claim AD as a side, D would need to be one of the vertices B or C, or a commonly recognized point forming part of the triangle’s defined structure. The provided figure and description do not support that AD exists within the given triangle framework, as no point D is defined within or connecting any existing vertices.
Therefore, according to the problem's context and based on the definition of the sides of a triangle, AD cannot be considered a side of triangle ABC. It follows that the statement "AD is a side of triangle ABC" should be deemed not true.
Answer:
Not true
Video Solution
Exercise #5
True or false:
BC is a side of triangle ABC.
Step-by-Step Solution
To solve this problem, we must determine whether BC is indeed a side of triangle ABC. A triangle consists of three vertices connected by three line segments that form its sides.
Firstly, observe the triangle labeled in the diagram with vertices A, B, and C. For triangle ABC, the sides are composed of the segments that connect these points.
- The three line segments connecting the vertices are:
- , connecting points A and B;
- , connecting points B and C; and
- , connecting points C and A.
Among these, BC is clearly listed as one of the segments connecting two vertices of the triangle. Therefore, BC is indeed a side of triangle ABC.
Hence, the statement is True.
Answer:
True
Video Solution
Frequently Asked Questions
How do you find the median of a triangle step by step?
+To find a triangle median: 1) Identify a vertex and the opposite side, 2) Find the midpoint of the opposite side by dividing its length by 2, 3) Draw a line segment from the vertex to this midpoint. This line segment is the median, and it divides the opposite side into two equal parts.
What is the difference between median, altitude, and angle bisector in triangles?
+A median connects a vertex to the midpoint of the opposite side. An altitude is perpendicular from a vertex to the opposite side. An angle bisector divides an angle into two equal parts. In equilateral triangles, all three are the same line, while in isosceles triangles, they coincide only for the vertex angle.
How many medians does every triangle have and where do they meet?
+Every triangle has exactly 3 medians - one from each vertex to the midpoint of the opposite side. All three medians always intersect at a single point called the centroid, which divides each median in a 2:1 ratio from vertex to midpoint.
What is the median to hypotenuse rule in right triangles?
+In a right triangle, the median drawn to the hypotenuse equals half the length of the hypotenuse. If the hypotenuse is 10 units, then the median to the hypotenuse is 5 units. This creates two equal segments from the right angle vertex to each end of the hypotenuse.
How do you calculate the area when a median divides a triangle?
+When a median divides a triangle, it creates two smaller triangles with equal areas. Each smaller triangle has an area equal to half the original triangle's area. Use the formula: Area = (base × height) ÷ 2, where the base is half the original side length.
What are the special properties of medians in isosceles triangles?
+In an isosceles triangle, the median drawn from the vertex angle (between the two equal sides) has special properties: it is also the altitude (height) and the angle bisector. This median is perpendicular to the base and divides the vertex angle into two equal parts.
How do you solve triangle median problems involving multiple medians?
+For problems with multiple medians: 1) Use the fact that medians bisect sides to find segment lengths, 2) Apply the equal area property - medians create triangles with equal areas, 3) Remember that all medians meet at the centroid, 4) Use specific triangle properties (right, isosceles, equilateral) when applicable.
What grade level typically learns about triangle medians in geometry?
+Triangle medians are typically introduced in middle school geometry (grades 7-8) and studied more extensively in high school geometry (grades 9-10). Students learn basic median properties first, then progress to more complex applications involving centroids and area calculations.