Triangle Height - Examples, Exercises and Solutions

Question Types:
Parts of a Triangle: Classify a triangle by its sidesParts of a Triangle: Is it possible...?Parts of a Triangle: Using the median to calculate the perimeterParts of a Triangle: Using the theorem: The median of a triangle divides it into two triangles of the same areaParts of a Triangle: Median in an isosceles triangle - propertiesParts of a Triangle: Using parallel linesParts of a Triangle: Determine the size of the given anglesParts of a Triangle: Identify the greater valueParts of a Triangle: Median in a right-angled triangleParts of a Triangle: Using properties of the medianParts of a Triangle: Identifying the sides in a triangle using median and heightParts of a Triangle: Calculate Angles in QuadrilateralsParts of a Triangle: True / falseParts of a Triangle: Identifying sides in a triangleParts of a Triangle: Using angles in a triangleParts of a Triangle: Identifying and defining elementsParts of a Triangle: Finding the size of angles in a triangle

Set the Height of a Triangle

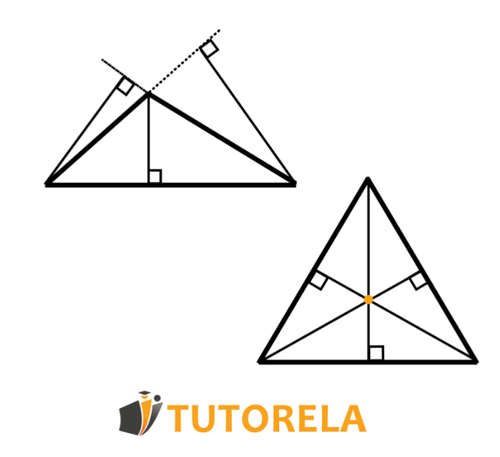
The height of a triangle is the segment that connects a vertex to the opposite side such that it creates a 90-degree angle.

In every triangle, there are three heights, as there are three vertices from which the height can be calculated relative to the side that is opposite to each of them.

The height can be found either inside or outside of the triangle. If it does not run through the interior of the triangle, it is called an external height.

Below, we provide you with some examples of triangle heights:

A1 - triangle height

Detailed explanation

Practice Triangle Height

Question 1

ABC is an isosceles triangle.

AD is the median.

What is the size of angle \( ∢\text{ADC} \)?

AAABBBCCCDDD

Question 2

Given the following triangle:

Write down the height of the triangle ABC.

AAABBBCCCEEEDDD

Question 3

Which of the following is the height in triangle ABC?

AAABBBCCCDDD

Question 4

Can a triangle have two right angles?

Question 5

Look at the two triangles below. Is EC a side of one of the triangles?

AAABBBCCCDDDEEEFFF

Examples with solutions for Triangle Height

Exercise #1

ABC is an isosceles triangle.

AD is the median.

What is the size of angle ∢ADC ∢\text{ADC} ?

AAABBBCCCDDD

Video Solution

Step-by-Step Solution

In an isosceles triangle, the median to the base is also the height to the base.

That is, side AD forms a 90° angle with side BC.

That is, two right triangles are created.

Therefore, angle ADC is equal to 90 degrees.

Answer

90

Exercise #2

Given the following triangle:

Write down the height of the triangle ABC.

AAABBBCCCEEEDDD

Video Solution

Step-by-Step Solution

An altitude in a triangle is the segment that connects the vertex and the opposite side, in such a way that the segment forms a 90-degree angle with the side.

If we look at the image it is clear that the above theorem is true for the line AE. AE not only connects the A vertex with the opposite side. It also crosses BC forming a 90-degree angle. Undoubtedly making AE the altitude.

Answer

AE

Exercise #3

Which of the following is the height in triangle ABC?

AAABBBCCCDDD

Video Solution

Step-by-Step Solution

Let's remember the definition of height of a triangle:

A height is a straight line that descends from the vertex of a triangle and forms a 90-degree angle with the opposite side.

The sides that form a 90-degree angle are sides AB and BC. Therefore, the height is AB.

Answer

AB

Exercise #4

Can a triangle have two right angles?

Video Solution

Step-by-Step Solution

The sum of angles in a triangle is 180 degrees. Since two angles of 90 degrees equal 180, a triangle can never have two right angles.

Answer

No

Exercise #5

Look at the two triangles below. Is EC a side of one of the triangles?

AAABBBCCCDDDEEEFFF

Video Solution

Step-by-Step Solution

Every triangle has 3 sides, let's go over the triangle on the left side:

Its sides are: AB, BC, CA

This means that in this triangle, side EC does not exist.

Let's go over the triangle on the right side:

Its sides are: ED, EF, FD

This means that in this triangle, side EC does not exist.

Therefore, EC is not a side in either of the triangles.

Answer

No.

Question 1

True or false?

\( \alpha+\beta=180 \)

αβ

Question 2

Find the measure of the angle \( \alpha \)

949494AAABBBCCC92

Question 3

Tree angles have the sizes 56°, 89°, and 17°.

Is it possible that these angles are in a triangle?

Question 4

Tree angles have the sizes:

90°, 60°, and 30.

Is it possible that these angles are in a triangle?

Question 5

Tree angles have the sizes:

50°, 41°, and 81.

Is it possible that these angles are in a triangle?


Exercise #6

True or false?

α+β=180 \alpha+\beta=180

αβ

Video Solution

Step-by-Step Solution

Given that the angles alpha and beta are on the same straight line and given that they are adjacent angles. Together they are equal to 180 degrees and the statement is true.

Answer

True

Exercise #7

Find the measure of the angle α \alpha

949494AAABBBCCC92

Video Solution

Step-by-Step Solution

It is known that the sum of angles in a triangle is 180 degrees.

Since we are given two angles, we can calculate a a

94+92=186 94+92=186

We should note that the sum of the two given angles is greater than 180 degrees.

Therefore, there is no solution possible.

Answer

There is no possibility of resolving

Exercise #8

Tree angles have the sizes 56°, 89°, and 17°.

Is it possible that these angles are in a triangle?

Video Solution

Step-by-Step Solution

Let's calculate the sum of the angles to see what total we get in this triangle:

56+89+17=162 56+89+17=162

The sum of angles in a triangle is 180 degrees, so this sum is not possible.

Answer

Impossible.

Exercise #9

Tree angles have the sizes:

90°, 60°, and 30.

Is it possible that these angles are in a triangle?

Video Solution

Step-by-Step Solution

Let's remember that the sum of angles in a triangle is equal to 180 degrees.

We'll add the three angles to see if their sum equals 180:

90+60+30=180 90+60+30=180

Therefore, these could be the values of angles in some triangle.

Answer

No.

Exercise #10

Tree angles have the sizes:

50°, 41°, and 81.

Is it possible that these angles are in a triangle?


Video Solution

Step-by-Step Solution

Let's remember that the sum of angles in a triangle is equal to 180 degrees.

We'll add the three angles to see if their sum equals 180:

50+41+81=172 50+41+81=172

Therefore, these cannot be the values of angles in any triangle.

Answer

Impossible.

Question 1

Tree angles have the sizes:

69°, 93°, and 81.

Is it possible that these angles are in a triangle?

Question 2

Tree angles have the sizes:

76°, 52°, and 52°.

Is it possible that these angles are in a triangle?

Question 3

Tree angles have the sizes:

31°, 122°, and 85.

Is it possible that these angles are in a triangle?

Question 4

Tree angles have the sizes 94°, 36.5°, and 49.5. Is it possible that these angles are in a triangle?

Question 5

Three angles measure as follows: 60°, 50°, and 70°.

Is it possible that these are angles in a triangle?

Exercise #11

Tree angles have the sizes:

69°, 93°, and 81.

Is it possible that these angles are in a triangle?

Video Solution

Step-by-Step Solution

Let's remember that the sum of angles in a triangle is equal to 180 degrees.

We'll add the three angles to see if their sum equals 180:

69+81+93=243 69+81+93=243

Therefore, these cannot be the values of angles in any triangle.

Answer

No.

Exercise #12

Tree angles have the sizes:

76°, 52°, and 52°.

Is it possible that these angles are in a triangle?

Video Solution

Step-by-Step Solution

Let's remember that the sum of angles in a triangle is equal to 180 degrees.

We will add the three angles to find out if their sum equals 180:

76+52+52=180 76+52+52=180

Therefore, these could be the values of angles in some triangle.

Answer

Yes.

Exercise #13

Tree angles have the sizes:

31°, 122°, and 85.

Is it possible that these angles are in a triangle?

Video Solution

Step-by-Step Solution

Let's remember that the sum of angles in a triangle is equal to 180 degrees.

We'll add the three angles to see if their sum equals 180:

31+122+85=238 31+122+85=238

Therefore, these cannot be the values of angles in any triangle.

Answer

Impossible.

Exercise #14

Tree angles have the sizes 94°, 36.5°, and 49.5. Is it possible that these angles are in a triangle?

Video Solution

Step-by-Step Solution

Let's remember that the sum of angles in a triangle is equal to 180 degrees.

We'll add the three angles to see if their sum equals 180:

94+36.5+49.5=180 94+36.5+49.5=180

Therefore, these could be the values of angles in some triangle.

Answer

Possible.

Exercise #15

Three angles measure as follows: 60°, 50°, and 70°.

Is it possible that these are angles in a triangle?

Video Solution

Step-by-Step Solution

Recall that the sum of angles in a triangle equals 180 degrees.

Let's add the three angles to see if their sum equals 180:

60+50+70=180 60+50+70=180

Therefore, it is possible that these are the values of angles in some triangle.

Answer

Possible.

Topics learned in later sections

  1. Area
  2. The sides or edges of a triangle
  3. The Sum of the Interior Angles of a Triangle
  4. Exterior angles of a triangle
  5. Types of Triangles
  6. Obtuse Triangle
  7. Equilateral triangle
  8. Identification of an Isosceles Triangle
  9. Scalene triangle
  10. Acute triangle
  11. Isosceles triangle
  12. The Area of a Triangle
  13. Area of a right triangle
  14. Area of Isosceles Triangles
  15. Area of a Scalene Triangle
  16. Area of Equilateral Triangles
  17. Perimeter
  18. Triangle
  19. Perimeter of a triangle