Constant Rate of Change

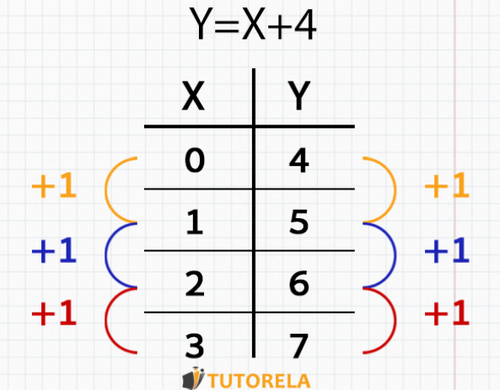
The meaning of the constant rate of change of a function can be seen when the variables $X$ change in fixed proportions and the $Y$ do as well.

For example, if the constant interval of the $X$ is $2$ and also that of the $Y$ is stable and does not vary from time to time.
The interval of the $Y$ variables does not necessarily have to be equal to that of the $X$ for it to be considered a case of constant rate of change.
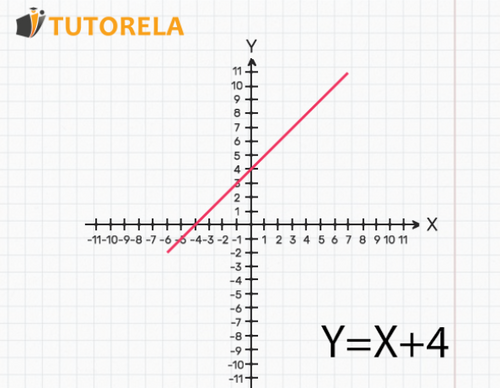
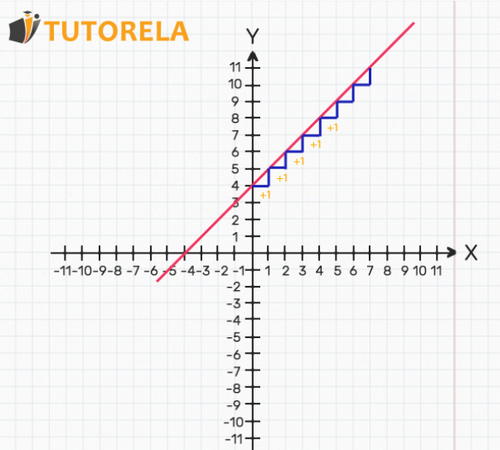
If the function is represented with a straight graph, it means that the rate of change is constant.
The rate of change is the slope of the function.

A constant rate of change is represented by a straight line, as seen in the following scheme:

A2 - Constant rate of change of a function

Detailed explanation

Start practice

Test yourself on variation of a function!

Look at the graph below and determine whether the function's rate of change is constant or not:

Practice more now

How can one identify the constant rate of change?

Let's see, the rate of change is constant if the following is true:

that when the variable $X$ increases from $4$ to $5$
and the $Y$ increases by $8$

then, when the variable $X$ grows from $102$ to $103$
also the $Y$ increases by $8$

Graph of the constant rate of change

Constant rate of change of a function

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Given the following graph, determine whether the rate of change is uniform or not?

Question 2

Given the following graph, determine whether the rate of change is uniform or not

Question 3

Given the following graph, determine whether the rate of change is uniform or not

Table of Constant Rate of Change

Representation of the function in table

Step graph of the constant rate of change

If you are interested in this article, you might also be interested in the following articles:

Rate of change of a function

Rate of change of a function represented graphically

Rate of change of a function represented by a table of values

Variable rate of change

Rate of change represented with steps in the function's graph

In the blog of Tutorela you will find a variety of articles with interesting explanations about mathematics

Examples and exercises with solutions of constant rate of change

Exercise #1

Look at the graph below and determine whether the function's rate of change is constant or not:

Video Solution

Step-by-Step Solution

First we need to remember that if the function is not a straight line, its rate of change is not constant.

The rate of change is not uniform since the function is not a straight line.

Answer

Not constant

Exercise #2

Given the following graph, determine whether the rate of change is uniform or not?

Video Solution

Step-by-Step Solution

Let's remember that if the function is not a straight line, its rate of change is not uniform.

Since the graph is not a straight line - the rate of change is not uniform.

Answer

Non-uniform

Exercise #3

Given the following graph, determine whether the rate of change is uniform or not

Video Solution

Step-by-Step Solution

The problem asks us to determine if the rate of change in the graph is uniform or not. To do this, we need to examine the graph closely to see whether it is linear.

If a graph is linear, it means it is a straight line, indicating a constant (uniform) rate of change. The slope of a straight line does not change, meaning that for every unit increase in $x$ there is a proportional and consistent change in $y$ .

In contrast, if a graph curves or the line is not straight, the rate of change would not be uniform. This is because a curve indicates that the amount $y$ changes for each unit change in $x$ is not constant.

By analyzing the given graph, we can see that it is a non-linear function with a visible curve. Since the line is not straight (it appears as a curved line in the graph), the rate of change of the function is not constant across its range.

Therefore, the solution to the problem is that the rate of change is non-uniform.

Consequently, the correct choice, corresponding to a non-uniform rate of change in the graph, is:

Non-uniform

Answer

Non-uniform

Exercise #4

Given the following graph, determine whether the rate of change is uniform or not

Video Solution

Step-by-Step Solution

To determine whether the rate of change in the graph is uniform, we must analyze the graph for consistency in slope across its span:

Step 1: Observe the graph shape.
Step 2: Check where the line is straight, showing no change in slope, and where it curves or changes slope, indicating non-uniform change.

Now, let's work through these steps:

Step 1: By visually inspecting the graph, note that it does not form a perfectly straight line but rather curves upwards. This indicates variability in the slopes along the graph.

Step 2: Since the graph curves, indicating that the slope is not the same throughout, we conclude that the rate of change is not constant.

The curvature implies that the rate of change is non-uniform, as it varies at different points along the x-axis. Therefore, the slope is inconsistent, confirming non-uniformity.

Therefore, the graph shows a non-uniform rate of change.

Answer

Non-uniform

Exercise #5

Given the following graph, determine whether the rate of change is uniform or not

Video Solution

Step-by-Step Solution

Let's remember that if the function is not a straight line, its rate of change is not uniform.

Since the graph is not a straight line - the rate of change is not uniform.

Answer

Non-uniform

Do you know what the answer is?

Question 1

Given the following graph, determine whether the rate of change is uniform or not

Question 2

Given the following graph, determine whether the rate of change is uniform or not?

Question 3

Given the following graph, determine whether function is constant

Start practice

Constant Rate of Change