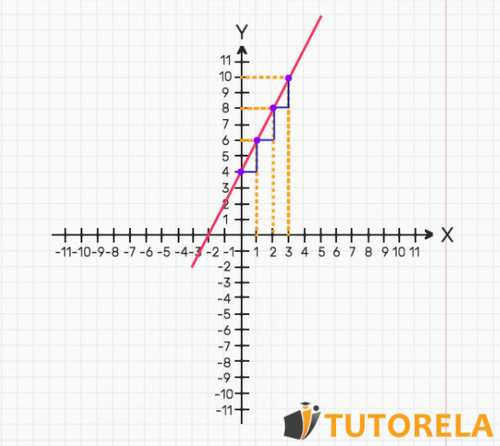
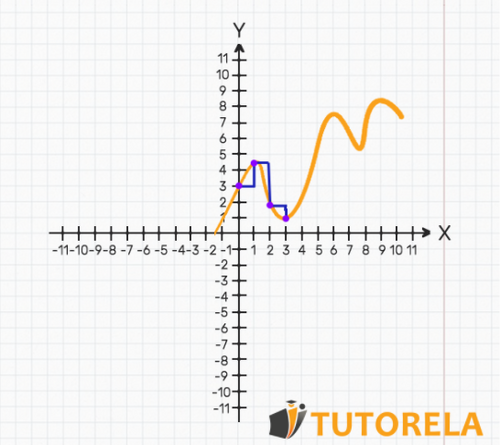
Rate of change represented with steps in the graph of the function

🏆Practice variation of a function
5 Questions
Functions
Variation of a Function
Practice
Add a new subject

Rate of change represented by steps in the function graph

We can draw stairs on the graph of the function to see the rate of change.
The base of the step will represent the interval in the X X variables and the height will symbolize the interval in the Y Y .

The step will mark the "jump" from X X in relation to the "jump" in Y Y .
The bases of the steps will always be the same since we always choose fixed intervals in X X .

  • If the heights of the steps are increasing, it means that the rate of change is increasing.
  • If the heights of the steps are decreasing, it means that the rate of change is decreasing.
  • If the heights of the steps do not change, it means that the rate of change is constant.
Start practice

Test yourself on variation of a function!

einstein

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Practice more now

To use this method, you need a graph paper on which we know the length and height of each square. In this way, you can draw "steps" across the entire graph, which will help us compare the height of these steps at different points of the function.

We will demonstrate this with two different graphs drawn on graph paper:

In the first one, there is a straight line in which all the heights of the steps are equal. Consequently, we understand that this is a constant rate of change.

Steps for Signaling a Constant Rate of Change

Steps for signaling a constant rate of change

The second graph represents a function in which the heights of the steps change.

Consequently, we understand that it is a rate of change that is not constant.  

Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Question 2

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Question 3

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Steps for Signaling a Non-Constant Rate of Change

image 2 Steps for signaling a non-constant rate of change

If you are interested in this article, you might also be interested in the following articles:

Rate of change of a function

Rate of change of a function represented graphically

Rate of change of a function represented by a table of values

Constant rate of change

Variable rate of change

In the blog of Tutorela you will find a variety of articles with interesting explanations about mathematics

Do you know what the answer is?
Question 1

Given the following graph, determine whether the rate of change is uniform or not

111222333444555666777888999101010111111121212131313141414151515111222333444555666777888000

Question 2

Given the following graph, determine whether the rate of change is uniform or not

–8–8–8–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888–3–3–3–2–2–2–1–1–1111222333444555666000

Question 3

Given the following graph, determine whether function is constant

–9–9–9–8–8–8–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666000

Start practice
Related Subjects
👉  Click here  to practice