Ways to Represent a Function

Representing a Function Verbally and with TablesGraphical Representation of a FunctionAlgebraic Representation of a FunctionNotation of a FunctionRepresentations of Functions - Examples, Exercises and Solutions
🏆Practice representations of functions
5 Questions
Functions
Representations of Functions
Practice
Add a new subject

Ways to represent a function

Functions can be represented in several ways, each providing a unique perspective on the relationship between inputs and outputs. Here are the primary methods:

Algebraic Representation

Representation using an equation of XX and YY, such as f(x)=2x+3f(x) = 2x + 3, showing how the output depends on the input.

Graphical representation

A visual representation on a coordinate plane, like using a graph, plotting on the XX and YY axis, where the function's behavior and trends (e.g., linear, quadratic) can be observed.

Tabular representation

A table of values that pairs inputs (xx) with corresponding outputs (yy) for a quick reference of specific points.

Verbal representation

A written explanation describing the relationship between variables, such as “The output is twice the input plus three.” Expressing the relationship between XX and YY using words.

Function notation

Functions can be written using different notations, such as Y=Y= or f(x)=f(x)=, both of which represent the output in terms of the input.

Four representations of the linear function F(x) = 2x + 3: algebraic formula, input-output table, graph on a coordinate plane, and verbal description

Start practice

Test yourself on representations of functions!

Is the given graph a function?

–4–4–4–3–3–3–2–2–2–1–1–1111222333444–2–2–2–1–1–1111222000

Practice more now

Ways to represent a function

Algebraic representation of a function

Before we talk about algebraic representation, it is important to understand what a function means.
A function describes the relationship between XX and YY.
In any function, XX is the independent variable and YY is the dependent variable. This means that every time we change XX, we get a different YY.
Y depends on XX and XX depends on nothing.

Important point: For each XX there will be only one YY!

An algebraic representation of a function is essentially the equation of the function.

Let's look at some examples of algebraic representation of a function and analyze them:
Y=X−3Y=X-3

In this equation, it is clear that YY depends on the XX we substitute into the equation.
If X=1X=1, then Y=−2Y=-2
If X=0X=0, then Y=−3Y=-3
If X=2X=2, then Y=−1Y=-1
In other words, the relationship between XX and YY is that YY will always be 33 less than XX.

Now let's examine another equation:
y=2x−5y=2x-5

Also in this equation, it is clear that YY depends on the XX we substitute into the equation.
If X=3X=3, then Y=1Y=1
If X=4X=4, then Y=3Y=3
If X=5X=5, then Y=−5Y=-5
In this equation, it is difficult to define in words the relationship between XX and YY, so we will say that the relationship between them is the equation itself:
y=2x−5y=2x-5

Now let's examine another equation:
y=xy=x

In this equation, it is also clear that YY depends on the XX we substitute into the equation.
If X=3X=3, then Y=3Y=3
If X=2X=2, then Y=2Y=2
If X=1X=1, then Y=1Y=1
The relationship between XX and YY is that they are identical each time.

Click here to learn more about the algebraic representation of a function!

Graphical representation of a function

A graphical representation of a function shows us how the function looks on the XX and YY axes.
What is most important to know?
For each XX, there is only one YY, and to draw a function as a graph, it is advisable to find at least 3 points of the function.
How to draw the function:
Each time, substitute a different XX into the algebraic representation and identify its YY. Mark all the points obtained on the drawing and then draw a straight line between them.

For example:
Y=3X−2Y=3X-2
Let's substitute three XXs and we get:

XXYY
0-2
11−1-1
244


Now let's mark the points we obtained on the number line:

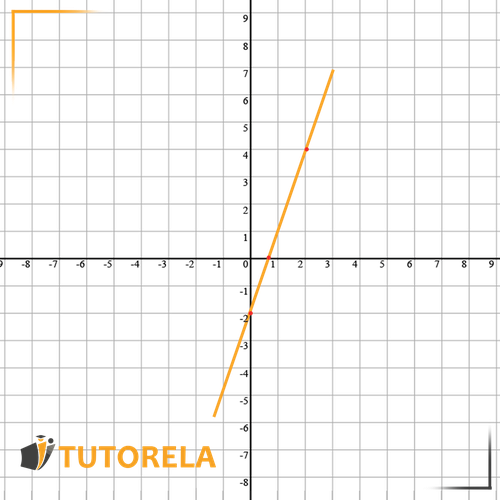
Linear Function Represention

Examples of graphical representation of a function:

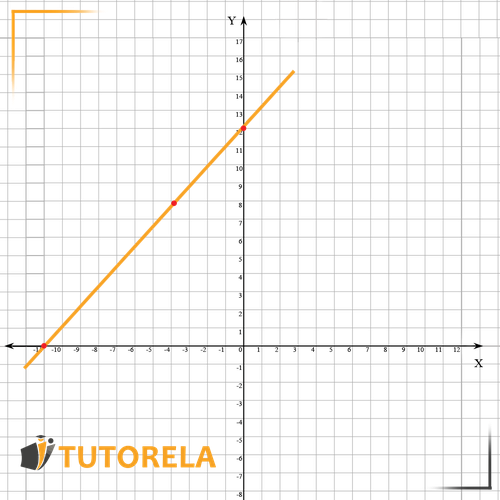
graphical representation of a linear function 1

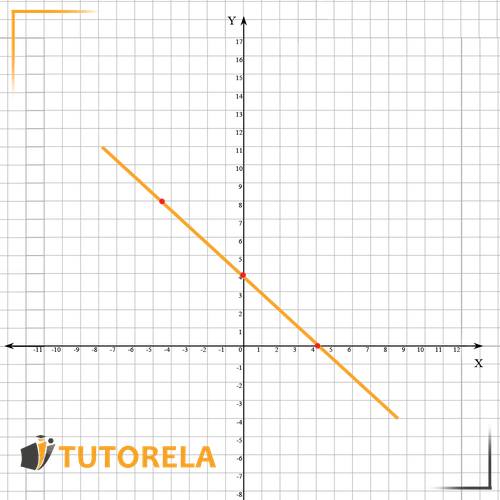
graphical representation of a linear function 2

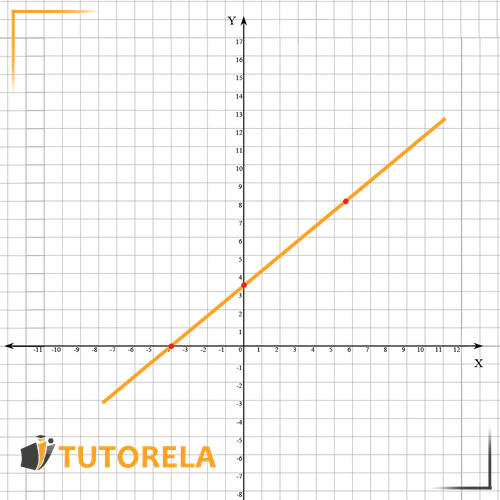
graphical representation of a linear function 3

Important tips:
How do you know if the function is increasing or decreasing?
There are 2 ways:

  1. According to the coefficient of XX in the algebraic representation – if the coefficient of XX is positive, the function increases from left to right. If negative, the function decreases from left to right.
  2. Mark 33 points of the function (substitute a different XX each time and find the YY) and then draw a straight line passing through them. Look from left to right and decide if the function is increasing or decreasing.

You can read more about the graphical representation of a function at this link!

Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Question 2

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Question 3

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Tabular representation of a function

A tabular representation is essentially a representation using a table of XX and YY showing us the value of YY for each XX that we substitute into the function.

Let's see an example:
For the algebraic representation - Y=4X−1Y=4X-1
we get a tabular representation like this:

YYXX
−1-1​0​​ 0​
3311
7722
111133
151544

Verbal representation of a function

A verbal representation of a function describes the relationship between XX and YY using words.

For example:
Each package of flour (XX) makes 33 whole pizzas (YY)

Y=3XY=3X

For more information on verbal and tabular representation of a function, click here!

Do you know what the answer is?
Question 1

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Question 2

Determine whether the given graph is a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Question 3

Does the graph below represent a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Function notation

How do we denote a function?
So far, we have denoted a function as Y=……Y=……
It is also useful to know that a function can be denoted in the following way:
F(x)=……...F(x)=……... which implies that we will get a value that depends on XX.

You can read more about function notation here!

Check your understanding
Question 1

Determine whether the following table represents a constant function:

XY02468-3-3-3-3-3

Question 2

Determine whether the following table represents a function

XY-226101416111621

Question 3

Determine whether the following table represents a constant function

XY-101247

Examples with solutions for Representations of Functions

Exercise #1

Is the given graph a function?

–4–4–4–3–3–3–2–2–2–1–1–1111222333444–2–2–2–1–1–1111222000

Video Solution

Step-by-Step Solution

To determine if the graph is a function, we will use the Vertical Line Test.

The Vertical Line Test states that a graph represents a function if and only if no vertical line intersects the graph at more than one point.

Let's apply this test to the given graph, where a horizontal line is drawn. This line represents the function the graph should be verified against.

  • Step 1: Conceptualize vertical lines passing through different x-values across the domain of the graph.
  • Step 2: Observe if any of these vertical lines intersect the graph at more than one point.

Upon inspection of the graph, we see that every vertical line intersects the graph at exactly one point.

This indicates that for every input (x-value), there is a unique output (y-value), fulfilling the criteria for the definition of a function.

Therefore, according to the Vertical Line Test, the given graph is indeed a function.

The correct choice is: Yes

Answer

Yes

Exercise #2

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Video Solution

Step-by-Step Solution

To determine whether the graph represents a function, we apply the Vertical Line Test. Here are the steps we follow:

  • Step 1: Visualize placing a vertical line across various parts of the graph.
  • Step 2: Check if the vertical line intersects the graph at more than one point at any given position.

Step 1: On evaluating the given graph carefully, there is a notable presence of a vertical line passing through multiple y-values. Specifically, the vertical line goes from y=−3 y = -3 to y=3 y = 3 at x=3 x = 3 .

Step 2: Since this vertical line at x=3 x = 3 intersects the graph at an infinite number of points, it fails the Vertical Line Test.

Therefore, the graph does not represent a function. According to our analysis and the Vertical Line Test, the correct answer is No.

Answer

No

Exercise #3

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Video Solution

Step-by-Step Solution

To determine if the graph in question represents a function, we'll employ the Vertical Line Test. This test helps to ascertain whether each input value from the domain (x-values) is connected to a unique output value (y-values).

  • According to the Vertical Line Test, a graph represents a function if no vertical line can intersect the graph at more than one point.
  • In the provided diagram, the graph is a straight line.
  • Visual inspection shows that any vertical line drawn at any point along the x-axis intersects the line exactly once.
  • This indicates that for each x-value, there is a unique corresponding y-value. Therefore, the relationship depicted by the graph meets the criteria for a function.

Thus, the given graph correctly characterizes a function.
Therefore, the solution to the problem is Yes.

Answer

Yes

Exercise #4

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Video Solution

Step-by-Step Solution

To determine if the given graph represents a function, we use the vertical line test: if any vertical line intersects the graph at more than one point, the graph is not a function.

Let's apply this test to the graph:

  • Examine different sections of the graph by drawing imaginary vertical lines.
  • Look for intersections where more than one point exists on the vertical line.

Upon examining the graph, we observe that there are several vertical lines that intersect the graph at multiple points, particularly in areas with loops or overlapping curves. This indicates that at those x x -values, there are multiple y y -values corresponding to them.

Since there exist such vertical lines, according to the vertical line test, the graph does not represent a function.

Thus, the solution to this problem is that the given graph is not a function.

Answer

No

Exercise #5

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Video Solution

Step-by-Step Solution

It is important to remember that a function is an equation that assigns to each element in domain X one and only one element in range Y

Let's note that in the graph:

f(0)=2,f(0)=−2 f(0)=2,f(0)=-2

In other words, there are two values for the same number.

Therefore, the graph is not a function.

Answer

No

Start practice

More Questions

Related Subjects
👉  Click here  to practice