Indefinite integral

An integral can be defined for all values (that is, for all $X$ ). An example of this type of function is the polynomial - which we will study in the coming years.

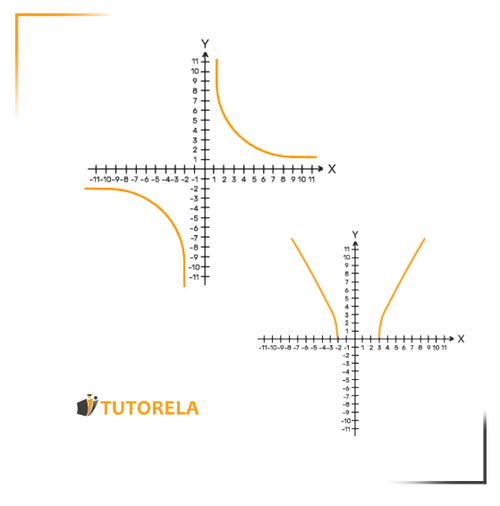
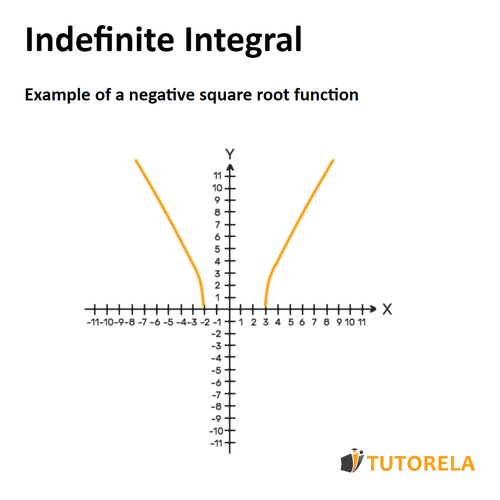
However, there are integrals that are not defined for all values (all $X$ ), since if we place certain $X$ or a certain range of values of $X$ we will receive an expression considered "invalid" in mathematics. The values of $X$ for which integration is undefined cause the discontinuity of a function.

Detailed explanation

Start practice

Test yourself on domain of a function!

$\frac{6}{x+5}=1$

What is the field of application of the equation?

Practice more now

An example of this is a function with a fraction with values $X$ in the denominator.
For example $1\over x$
According to mathematical rules, the denominator of a fraction cannot be zero since it is not possible to divide by zero. Therefore, when there is a possibility that the denominator equals zero, the integral cannot be defined for the values of $X$ that could cause the denominator to be zero.

Another example is a square root function. For example
According to the algebraic rules, the expression under the square root cannot be negative, that is, it must be positive or zero, but in no way negative. Therefore, The integral will be undefined for a range of values of $X$ that cause the expression under the square root to be negative. $f(x)=\sqrt{x^2-x-5}$