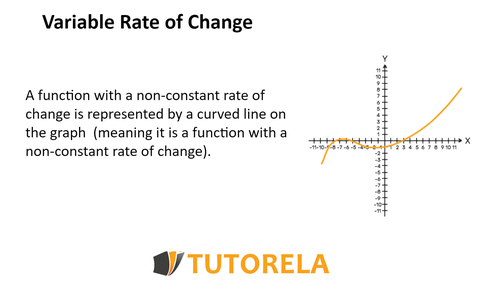
Rate of change of a function represented graphically

🏆Practice variation of a function
5 Questions
Functions
Variation of a Function
Practice
Add a new subject

Rate of Change of a Function Represented Graphically

The rate of change of a function represented graphically allows us to determine in a much more intuitive way whether it is a constant (fixed) or inconstant (not fixed) rate, and also if it is a faster (steeper slope) or slower (more moderate slope) rate.

The following graph can demonstrate the aforementioned in the best way:

Rate of Change of a Function Represented Graphically

1- Rate of Change of a Function Represented Graphically

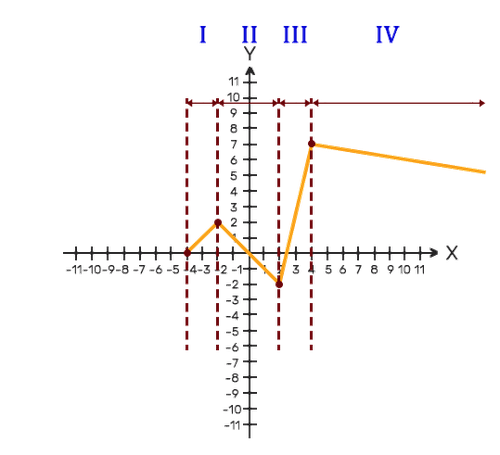
Let's observe the graph. We will notice that it is divided into 4 different branches. Now we will analyze each of the branches:

  • Branch 1: the graph rises (increasing function) at a constant rate (straight line).
  • Branch 2: The graph falls (decreasing function) at a constant rate (straight line).
  • Branch 3: the graph rises (increasing function) at a constant rate (straight line) and more quickly than branch 1 (the slope is steeper).
  • Branch 4: The graph falls (decreasing function) at a constant rate (straight line) and more slowly than branch 2 (the slope is more moderate).
Start practice

Test yourself on variation of a function!

einstein

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Practice more now

We were able to capture all this information just through the graph of the function.

(Rate of change of a function: a function with a constant rate of change that when represented by a straight line on the graph means that it is a function with a constant rate of change)

We can see the rate of change of the function graphically.
First, to display it graphically, we will observe the function and examine whether the slope rises or falls.
The slope is the coefficient of X X .
If the coefficient is positive: the slope rises and the function will be increasing.
If the coefficient is negative: the slope falls and the function will be decreasing.

Next, we will examine what the independent variable in the function is if there is one and mark it as the point of intersection with the Y Y axis.
Another way to plot the function is to control what its point of intersection with the X X axis (set y=0 y=0 ) and the Y Y axis (set X=0 X=0 ) is and draw it accordingly.
A function that appears in the graphical representation as a straight line will have a constant rate of change.
A function that appears in the graphical representation as a line that is not straight will have an inconsistent rate of change.

If you are interested in this article, you might also be interested in the following articles:

Functions for Seventh Grade

Rate of Change of a Function

Rate of Change of a Function Represented by a Table of Values

Constant Rate of Change

Variable Rate of Change

Rate of Change Represented with Steps in the Function Graph

In the blog of Tutorela you will find a variety of articles with interesting explanations about mathematics

Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Question 2

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Question 3

Given the following graph, determine whether the rate of change is uniform or not

–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888999101010111111–3–3–3–2–2–2–1–1–1111222333444555000

Start practice
Related Subjects
👉  Click here  to practice