Median in a triangle

A median in a triangle is a line segment that extends from a vertex to the midpoint of the opposite side, dividing it into two equal parts.

Additional properties:

In every triangle, it is possible to draw 3 medians.
All 3 medians intersect at one point.
The median to a side in a triangle creates 2 triangles of equal area.
In an equilateral triangle - the median is also a height and an angle bisector.
In an isosceles triangle - the median from the vertex angle is also a height and an angle bisector.
In a right triangle - the median to the hypotenuse equals half the hypotenuse.

Diagram of triangle ABC showing medians AD, BE, and CF intersecting at the centroid. The centroid divides each median into a 2:1 ratio, illustrating triangle centroid properties.

Detailed explanation

Start practice

Test yourself on parts of a triangle!

Can a triangle have a right angle?

Practice more now

Median in a triangle

In this article, we will learn everything you need to know about medians in a triangle! Don't worry, the material about medians in a triangle is both easy and straightforward to understand.

Define a median in a triangle?

A median in a triangle is a line segment that extends from a vertex to the midpoint of the opposite side, dividing it into two equal parts.
Remember that "median" in real life represents the middle point, and similarly here it divides the side in the middle!

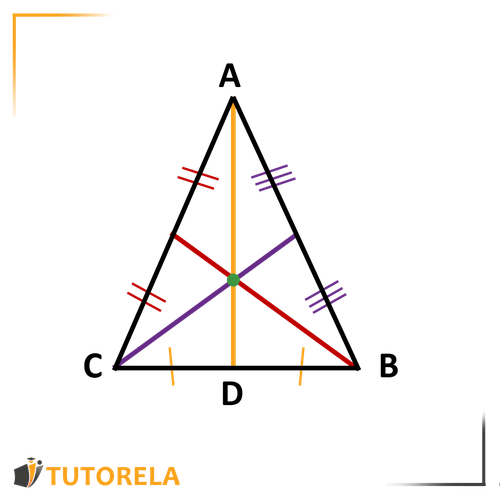
We can observe this in the following drawing:

Diagram of a triangle ABC with a median AD drawn from vertex A to the midpoint D of side BC, illustrating geometric properties of medians.

In triangle $ABC$
$AD$ is a median - it extends from the vertex $A$ and divides the opposite side $CB$ into two
equal parts: $CD=BD$

Additional Properties of a Median in a Triangle:

In every triangle, it is possible to draw 3 medians.
All 3 medians intersect at one point.
The median to a side of a triangle creates 2 triangles of equal area.

You can observe this below:

Since there are 3 vertices in a triangle, there can be 3 medians.
Each median extends from a vertex to the opposite side and bisects it.
All medians intersect at one point.

Reminder:
How do we calculate the area of a triangle?

$height*corresponding~side~to~height \over 2$

If we take for example the triangle $ABC$ and want to calculate its area when:
$AD$ height = $6$
$BC = 8$

Diagram of triangle ABC with median AD labeled. The length of median AD is shown as 6 units, and segment BD is labeled as 4 units, highlighting the geometric properties of a triangle's median.

We can deduce that the area of triangle $ABC$ is:
$\frac{6*8}{2}=24$
Now if we draw the median $AD$ we can observe that the two triangles it creates are equal in area.
The side is divided in the middle thus it is identical in both triangles and the height is identical.
Therefore, the area of each created triangle is identical and will be equal to half the area of triangle $ABC$

$\frac{6*4}{2}=12$

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Is the straight line in the figure the height of the triangle?

Question 2

Is the straight line in the figure the height of the triangle?

Question 3

Can a plane angle be found in a triangle?

3 important statements about medians:

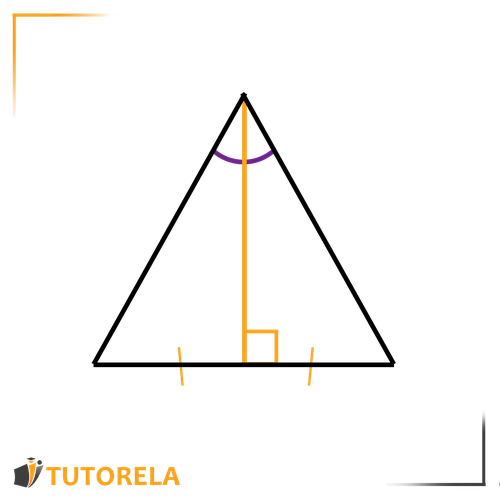
In an equilateral triangle - the median is also a height and an angle bisector.
As shown in the figure:

$AD$ is a height to side $CB$
and also a median to side $CB$ (divides it into two equal parts)
as well as an angle bisector

Diagram of an isosceles triangle with a median intersecting the base at a right angle. The median forms a perpendicular bisector, and the top angle is highlighted in purple.

$A$

In an isosceles triangle - the median drawn from the vertex angle is also a height and an angle bisector.
Let's observe this in the figure below:

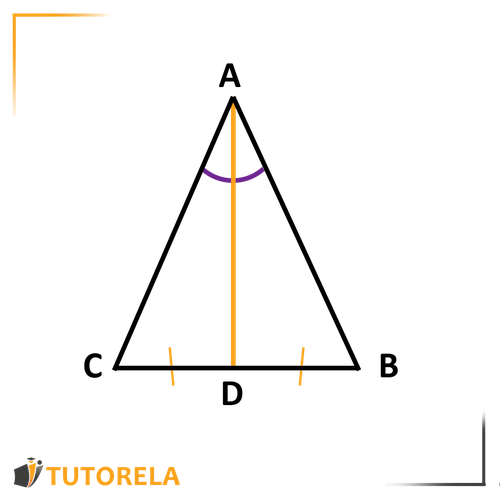
In an isosceles triangle - the median drawn from the vertex angle is also a height and an angle bisector.

$AD$ is a median drawn from vertex angle $A$ .
It is also a height to side $CB$ , as well as a median to $CB$ , in addition to bisecting the vertex angle $A$ .

3. In a right triangle - the median to the hypotenuse equals half the hypotenuse.

We can observe this in the figure below:

Triangle $ABC$ is a right triangle.
$CD$ is the median to the hypotenuse and equals half of the hypotenuse.
That is
$CD=AD=DB$

Exercise:

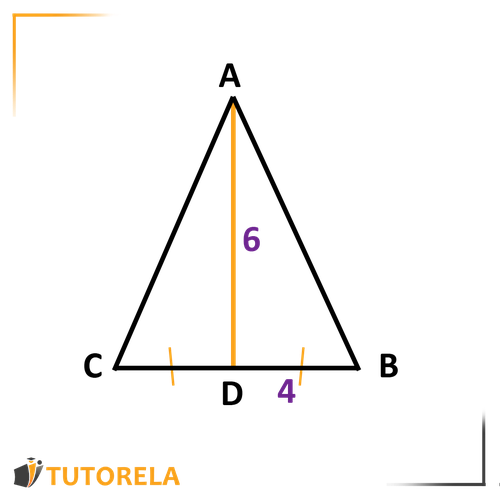
Given:

$CD$ is a median in triangle $ABC$
$CE$ is a median in triangle $ACD$

$AB=14$

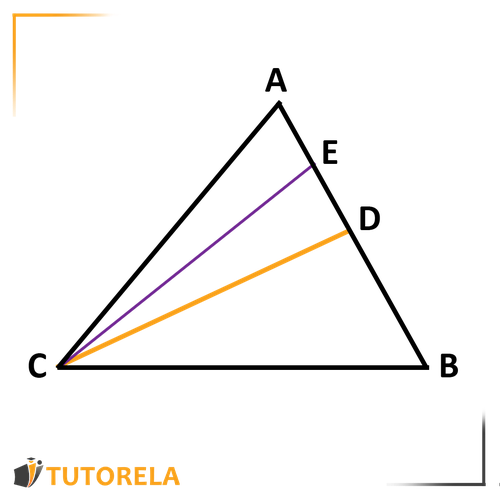
Diagram of a triangle with medians AD and CE drawn in orange and purple, intersecting at a single point inside the triangle. The vertices are labeled A, B, and C, while the midpoints of the sides are labeled D and E.

Calculate the length of segment $AE$ .
Determine the area of triangle $ECD$ if it is known that the area of triangle $ACE$ is $6$ ?
Based on your answer in part b, determine the area of triangle $DCB$

Solution:

Let's mark the given information in the drawing.

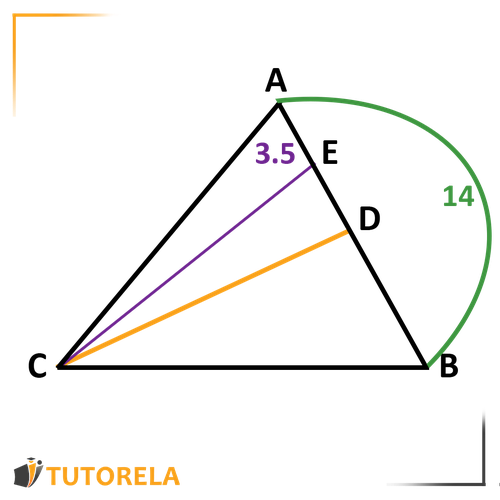
Diagram of a triangle labeled A, B, and C, with medians AD (orange) and CE (purple). The length of CE is marked as 3.5. A green arc labeled 14 spans from vertex A to vertex B, highlighting the angle subtended by side AB.

Given that – $AB =14$
Since $CD$ is a median,
$AD=DB=7$
due to the fact that the median bisects the side at its midpoint.
Given that $CE$ is also a median.
Therefore $AE=ED=3.5$ .

2. Given that the area of triangle $ACE$ is $6$
The area of triangle $ECD$
must also be $6$ . A median divides the triangle into two triangles of equal area.

3. The area of triangle $DCB$ must be equal to the area of triangle $ACD$ .

Triangle $ACD$ consists of two triangles with equal areas that sum up to $12$ .
Therefore, the area of triangle $DCB$ is $12$ .

Do you know what the answer is?

Question 1

Is the straight line in the figure the height of the triangle?

Question 2

Is the straight line in the figure the height of the triangle?

Question 3

Is the straight line in the figure the height of the triangle?

Examples with solutions for Parts of a Triangle

Exercise #1

Is the straight line in the figure the height of the triangle?

Video Solution

Step-by-Step Solution

The triangle's altitude is a line drawn from a vertex perpendicular to the opposite side. The vertical line in the diagram extends from the triangle's top vertex straight down to its base. By definition of altitude, this line is the height if it forms a right angle with the base.

To solve this problem, we'll verify that the line in question satisfies the altitude condition:

Step 1: Identify the triangle's vertices and base. From the diagram, the base appears horizontal, and the vertex lies directly above it.
Step 2: Check the nature of the line. The line is vertical when the base is horizontal, indicating perpendicularity.
Conclusion: The vertical line forms right angles with the base, thus acting as the altitude or height.

Therefore, the straight line depicted is indeed the height of the triangle. The answer is Yes.

Answer

Yes

Exercise #2

Can a triangle have a right angle?

Video Solution

Step-by-Step Solution

To determine if a triangle can have a right angle, consider the following explanation:

Definition of a Right Angle: An angle is classified as a right angle if it measures exactly $90^\circ$ .
Definition of a Right Triangle: A right triangle is a type of triangle that contains exactly one right angle.
According to the definition, a right triangle specifically includes a right angle. This is a well-established classification of triangles in geometry.

Thus, a triangle can indeed have a right angle and is referred to as a right triangle.

Therefore, the solution to the problem is Yes.

Answer

Yes

Exercise #3

Is the straight line in the figure the height of the triangle?

Video Solution

Step-by-Step Solution

To determine if the straight line is the height of the triangle, we'll analyze its role within the triangle:

Step 1: Observe the triangle and the given line. The triangle seems to be made of three sides and a vertical line within it.
Step 2: Recall that the height of a triangle, in geometry, is defined as a perpendicular dropped from a vertex to the opposite side.
Step 3: Examine the positioning of the line: The vertical line starts at one vertex of the triangle and intersects the base, appearing to be perpendicular.
Step 4: Verify perpendicularity: Given that the line is shown as a clear vertical (and a small perpendicular indicator suggests perpendicularity), we accept this line as the height.
Step 5: Conclude with verification that the line is effectively meeting the definition of height for the triangle in the diagram.

Therefore, the vertical line in the figure is indeed the height of the triangle.

Yes

Answer

Yes

Exercise #4

Is the straight line in the figure the height of the triangle?

Video Solution

Step-by-Step Solution

In the given problem, we have a triangle depicted with a specific line drawn inside it. The question asks if this line represents the height of the triangle. To resolve this question, we need to discern whether the line is perpendicular to one of the sides of the triangle when extended, as only a line that is perpendicular from a vertex to its opposite side can be considered the height.

The line in question is shown intersecting one of the sides within the triangle but does not form a perpendicular angle with any side shown or the ground (as is required for it to be the height of the triangle). A proper height would typically intersect perpendicularly either at or along the extended line of the opposite side from a vertex.

Therefore, based on the visual clues provided and the typical geometric definition of a height (or altitude) in a triangle, this specific line does not fit the criteria for being a height.

Thus, we conclude that the line depicted is not the height of the triangle. The correct answer is No.

Answer

Exercise #5

Is the straight line in the figure the height of the triangle?

Video Solution

Step-by-Step Solution

The height of a triangle is defined as the perpendicular distance from a vertex to the line containing the opposite side (base). In this problem, we observe a vertical line segment drawn from a point on the base (horizontal line at the bottom of the triangle) to some level above the base. To determine if this line is a height, it must be perpendicular to the base and also reach to the opposite vertex of the triangle.

In the provided figure, the vertical line extends vertically from the base but does not connect to the opposite vertex of the triangle (at the top). Instead, it terminates at some intermediate point above the base. Since the line does not satisfy the full condition of being perpendicular and reaching an opposite vertex, it cannot be considered the height of this triangle.

Therefore, the given straight line is not the height of the triangle.

The correct and final answer is: No.

Answer

Start practice

Median in a triangle

Median in a triangle

Test yourself on parts of a triangle!

Median in a triangle

Define a median in a triangle?

3 important statements about medians:

Exercise:

Examples with solutions for Parts of a Triangle

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

More Questions

Parts of a Triangle