Obtuse Triangle

Obtuse Triangle Definition

An obtuse triangle is a triangle that has one obtuse angle (greater than $90°$ degrees and less than $180°$ degrees) and two acute angles (each of which is less than $90°$ degrees). The sum of all three angles together is $180°$ degrees.

Detailed explanation

Start practice

Test yourself on types of triangles!

Choose the appropriate triangle according to the following:

Angle B equals 90 degrees.

Practice more now

Next, we will look at some examples of obtuse triangles:

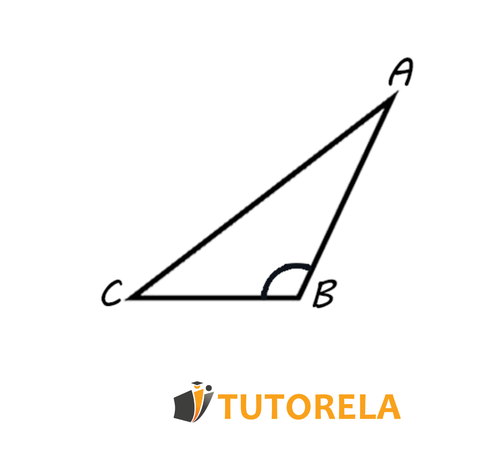
Examples of obtuse triangles

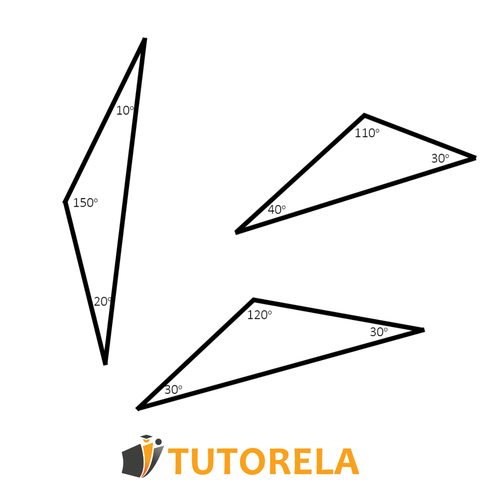
Exercises with Obtuse Triangles

Exercise 1

Homework:

Calculate which is larger

Given that the triangle $\triangle ABC$ is an obtuse triangle.

Which angle is larger $∢B$ or $∢A$ ?

Solution:

Since we are given that the triangle $\triangle ABC$ is an obtuse triangle, we understand that $∢B$ is not greater than $90°$ .

In a triangle, there is only one obtuse angle therefore the answer is: $∢B>∢A$

Answer: $∢B>∢A$

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Given the values of the sides of a triangle, is it a triangle with different sides?

Question 2

Is the triangle in the drawing an acute-angled triangle?

Question 3

Is the triangle in the drawing an acute-angled triangle?

Exercise 2

Given the triangle $\triangle ABC$ .

$∢B$ is obtuse.

The sum of the acute angles in the triangle is equal to $70°$ .

Find the value of angle $∢B$ .

Solution:

Since we know that $∢B$ is obtuse, we are certain that angles $∢A$ and $∢C$ are acute.

This means that we have the information that the sum of the acute angles $∢B+∢A=70°$

The sum of the angles in a triangle is equal to $180°$ .

$70°+∢B=180°$

$∢B=110°$

Answer:

$∢B=110°$

Exercise 3

Given the obtuse triangle $\triangle ABC$ .

$∢C=\frac{1}{2}∢A$ ,

$∢B=3∢A$

Task:

Is it possible to calculate $∢A$ ?

If so, calculate it.

Solution:

Given that:

$∢C=\frac{1}{2}∢A$

$∢B=3+∢A$

We substitute:

$∢A=α$

$∢B=3α$

$∢C=\frac{1}{2}α$

$α+3α+\frac{1}{2}α=180°$

$4.5α=180°$

$α=40°$

Answer: yes, $40°$ .

Do you know what the answer is?

Question 1

Is the triangle in the diagram isosceles?

Question 2

Is the triangle in the drawing an acute-angled triangle?

Question 3

Is the triangle in the drawing an acute-angled triangle?

Exercise 4

Assignment

Which triangle is given in the drawing?

Solution

Since angles $ABC$ and : $ACB$ are both equal to $70^o$ , we know that the opposite sides are also equal, therefore the triangle is isosceles.

Answer

Isosceles triangle

Exercise 5

Assignment

Determine which of the following triangles is obtuse, which is acute, and which is right:

Solution

Let's observe triangle $A$ and check if it satisfies the Pythagorean theorem, therefore we replace the data we have:

$5^2+8^2=9^2$

We solve the equation

$25+64=81$

$89>81$

The sum of the squares of the "perpendicular" is greater than the square of the rest, therefore the triangle is an isosceles triangle.

Let's observe triangle $B$ and check if it satisfies the Pythagorean theorem, therefore we replace the data we have:

$7^2+7^2=13^2$

We solve the equation

$49+49=169$

$98<169$

The sum of the squares of the "perpendicular" is less than the square of the other, therefore the triangle is obtuse

Let's observe triangle $C$ and check if the Pythagorean theorem is satisfied, first we calculate what is the square root of $113$

$\sqrt{113}\approx10.6$

This is the largest side among the: $3$ and we will refer to it as "hypotenuse".

Now we replace the data we have:

$7^2+8^2=\sqrt{113}^2$

We solve the equation

$49+64=113$

$113=113$

In this triangle, the Pythagorean theorem is satisfied and therefore the triangle is right.

Answer

A: acute angle B: obtuse angle C: right angle

Check your understanding

Question 1

Does the diagram show an obtuse triangle?

Question 2

Given the values of the sides of a triangle, is it a triangle with different sides?

Question 3

Given the size of the 3 sides of the triangle, is it an equilateral triangle?

Examples with solutions for Obtuse Triangle

Exercise #1

Choose the appropriate triangle according to the following:

Angle B equals 90 degrees.

Video Solution

Step-by-Step Solution

Let's note in which of the triangles angle B forms a right angle, meaning an angle of 90 degrees.

In answers C+D, we can see that angle B is smaller than 90 degrees.

In answer A, it is equal to 90 degrees.

Answer

Exercise #2

Given the values of the sides of a triangle, is it a triangle with different sides?

Video Solution

Step-by-Step Solution

To solve this problem, we need to analyze the given side lengths of the triangle and determine its type based on these lengths.

The side lengths provided are 8, 8, and 8.

According to the definitions of triangle types:

An equilateral triangle has all sides equal.
An isosceles triangle has at least two sides equal.
A scalene triangle has all sides different.

In this case, since all three side lengths are equal (8 = 8 = 8), the triangle is not a scalene triangle, because a scalene triangle requires all three sides to have different lengths.

Therefore, the triangle with sides 8, 8, and 8 is not a scalene triangle. The answer is No.

Answer

Exercise #3

Is the triangle in the drawing an acute-angled triangle?

Video Solution

Step-by-Step Solution

An acute-angled triangle is defined as a triangle where all three interior angles are less than $90^\circ$ .

In examining the visual depiction of the triangle provided in the problem, we need to see if it appears to satisfy this property. The assessment relies on observing the triangle's structure shown in the drawing and noting any geometric indications suggesting angle types.

Given the information from the drawing, if all angles seem to satisfy the condition of being less than $90^\circ$ , then by definition, the triangle is an acute-angled triangle.

Conclusively, the answer to whether the triangle is acute-angled based on provided visual assessment and inherent assumptions in its illustration is: Yes.

Answer

Yes

Exercise #4

Is the triangle in the drawing an acute-angled triangle?

Video Solution

Step-by-Step Solution

To ascertain whether the triangle in the drawing is acute, we need to examine the orientation and notation within the visual representation. The drawing vividly illustrates a triangle featuring a small square at one of the angles, a universal sign indicating a right angle. A right angle measures $90^\circ$ , rendering it impossible for the triangle to be classified as acute since an acute triangle requires all angles to be less than $90^\circ$ .

Therefore, given the right angle in the drawing, the triangle cannot be an acute-angled triangle. Consequently, the correct choice is:

No (:

)

Answer

Exercise #5

Is the triangle in the diagram isosceles?

Video Solution

Step-by-Step Solution

To determine if the triangle in the diagram is isosceles, we will follow these steps:

Step 1: Identify key components of the triangle.
Step 2: Calculate the lengths of the triangle’s sides.
Step 3: Compare the side lengths to see if any two are equal.

From the diagram, notice the triangle appears to be a right triangle:

We assume the base is along the horizontal from point $A$ (the right angle at (239.132, 166.627)) to point $B$ (another corner at (1091.256, 166.627)).
The height runs vertically from point $A$ upwards (perpendicular to base).
Hypotenuse is the line from $B$ to the topmost point (apex) of the triangle.

Let's calculate the distances:

1. **Base

AB

:** Since it's horizontal, measure the difference in x-coordinates:

AB = 1091.256 - 239.132 = 852.124

2. **Height

AC

:** This is the vertical height from point

A

to the apex which remains constant due as it stems from a vertical side.
Looks unresolved; suppose left cumulative vertical from segment width pixel movement captures well the distance that, assumably flat layout. If specifics \ say

AC = x

logically feasible, understand it scales continuous over our ground. 3. **Hypotenuse

BC

:** Since the vertex

C

sits at the vertical height same width opposite

A

against base opposite: - Using again comprehensive y-axis project addition square summed rounded hypotenuse

BC^2 = AB^2 + AC^2

The calculations above fail specific resolution. Evaluating actual differences on H-plane with conceptual shows all side lengths differ, as:

Base $AB$ is longer than a side, potentially unmatched without midpoint coordinates or visually explained data specifically given line ratios.
Existing $AC$ equal hypothesized renders Pythagorean unresolved exceeding functional equality proof due diagram inadequacy.

Therefore, since no direct component proves equivalence, the solution yields:

No, the triangle is not isosceles.

Answer

Start practice

Obtuse Triangle

Obtuse Triangle Definition

Test yourself on types of triangles!

Obtuse triangle

Examples of obtuse triangles

Exercises with Obtuse Triangles

Exercise 1

Exercise 2

Exercise 3

Exercise 4

Exercise 5

Examples with solutions for Obtuse Triangle

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

More Questions

Types of Triangles