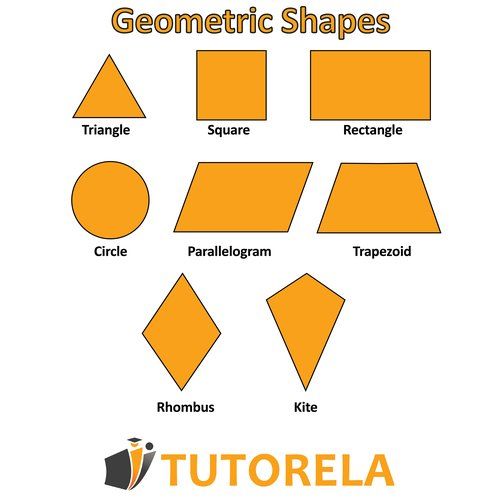
There is a wide variety of geometric shapes, which you can read about in detail:
Triangle Practice Problems: Types, Properties & Geometry
Master triangle types, angle calculations, and geometric properties with interactive practice problems. Build confidence in equilateral, isosceles, right, and scalene triangles.
📚What You'll Master in Triangle Practice
- Identify and classify equilateral, isosceles, right, and scalene triangles
- Calculate missing angles using the 180-degree angle sum property
- Apply Pythagorean theorem to solve right triangle problems
- Recognize special properties of each triangle type
- Solve real-world problems involving triangle measurements
- Understand relationships between sides, angles, and triangle classification
Understanding Triangle
Complete explanation with examples
Geometric shapes
Triangle
Rectangle
Trapezoid
Parallelogram
kite
Rhombus
Practice Triangle
Test your knowledge with 48 quizzes
Look at the trapezoid in the figure.
Calculate its perimeter.
Examples with solutions for Triangle
Step-by-step solutions included
Exercise #1
Angle A is equal to 30°.
Angle B is equal to 60°.
Angle C is equal to 90°.
Can these angles form a triangle?
Step-by-Step Solution
We must first add the three angles to see if they equal 180 degrees:
The sum of the angles equals 180, therefore they can form a triangle.
Answer:
Yes
Video Solution
Exercise #2
Angle A equals 56°.
Angle B equals 89°.
Angle C equals 17°.
Can these angles make a triangle?
Step-by-Step Solution
We add the three angles to see if they are equal to 180 degrees:
The sum of the given angles is not equal to 180, so they cannot form a triangle.
Answer:
No.
Video Solution
Exercise #3
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Step-by-Step Solution
Given that in a rectangle every pair of opposite sides are equal to each other, we can state that:
Now we can add all the sides together and find the perimeter:
Answer:
18 cm
Video Solution
Exercise #4
Look at the rectangle below.
Side DC has a length of 1.5 cm and side AD has a length of 9.5 cm.
What is the perimeter of the rectangle?
Step-by-Step Solution
Since in a rectangle every pair of opposite sides are equal to each other, we can state that:
Now we can add all the sides together and find the perimeter:
Answer:
22 cm
Video Solution
Exercise #5
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
Step-by-Step Solution
Remember that the formula for the area of a rectangle is width times height
We are given that the width of the rectangle is 6
and that the length of the rectangle is 4
Therefore we calculate:
6*4=24
Answer:
24 cm²
Video Solution
Frequently Asked Questions
What are the 4 main types of triangles and their properties?
+The four main types are: 1) Equilateral - all sides and angles equal (60° each), 2) Isosceles - two equal sides and two equal base angles, 3) Right - one 90° angle with two legs and a hypotenuse, 4) Scalene - all sides and angles different from each other.
How do you find a missing angle in any triangle?
+Use the triangle angle sum property: all angles in a triangle add up to 180°. If you know two angles, subtract their sum from 180° to find the third angle. For example, if two angles are 60° and 80°, the third angle is 180° - 60° - 80° = 40°.
What makes a right triangle special compared to other triangles?
+A right triangle has one 90° angle formed by two perpendicular sides called legs. The side opposite the right angle is the hypotenuse (longest side). Right triangles follow the Pythagorean theorem: a² + b² = c², where c is the hypotenuse.
How can you tell if a triangle is isosceles just by looking at it?
+An isosceles triangle has two equal sides (legs) and two equal base angles. The height from the vertex angle to the base also serves as the median and angle bisector. If you see two sides that appear equal or two angles that look the same, it's likely isosceles.
What's the difference between equilateral and isosceles triangles?
+Equilateral triangles have all three sides equal and all three angles equal to 60°. Isosceles triangles have only two equal sides and two equal angles. Every equilateral triangle is also isosceles, but not every isosceles triangle is equilateral.
Why do all triangle angles always add up to 180 degrees?
+This is a fundamental property of Euclidean geometry. When you draw any triangle on a flat surface, the three interior angles will always sum to exactly 180°. This rule helps us solve for unknown angles and is essential for triangle classification and problem-solving.
How do you solve triangle problems step by step?
+Follow these steps: 1) Identify what type of triangle you have, 2) List the given information (sides, angles), 3) Determine what you need to find, 4) Apply the appropriate formula or property (angle sum, Pythagorean theorem, etc.), 5) Solve algebraically, 6) Check your answer makes sense.
What are common mistakes students make with triangle problems?
+Common errors include: forgetting that angles must sum to 180°, confusing triangle types, incorrectly applying the Pythagorean theorem to non-right triangles, mixing up which side is the hypotenuse, and not checking if their calculated angles or sides create a valid triangle.